Đề thi cuối kì II, 2022 - 2023

Câu 1

1.1. Các thuật toán sắp xếp nào, trong số các thuật toán insertion sort, heap sort, merge sort và quick sort, được thiết kế theo chiến lược chia để trị? (0.5 điểm)

1.2. Cho dãy số A = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Hãy cho biết:

a. Những thuật toán sắp xếp nào, trong số các thuật toán heap sort, quick sort và merge sort, sẽ gặp thuận lợi khi sắp dãy số A theo thứ tự giảm dần? (0.5 điểm)

b. Thuận lợi đó, theo từng thuật toán đã trả lời ở câu 1.2 a, là gì? (0.5 điểm)

Bài làm tham khảo

1.1. Các thuật toán sắp xếp thiết kế theo chiến lược chia để trị là: merge sort và quick sort

1.2. Các thuật toán sắp xếp thuận lợi cho một dãy số đã giảm dần bao gồm heap sort và quick sort.

• Với heap sort, mảng đã cho là 1 cây min-heap sẵn, khi thực hiện thao tác heapify, không có hoán đổi phần tử xảy ra.
• Với quick sort, ta sẽ luôn lấy được phần tử trung vị, gần trung vị khi chọn pivot là phần tử giữa mảng.

Câu 2

Telegram đã ra đời được 10 năm và được biết đến như là một dịch vụ nhắn tin tức thời miễn phí, đa nền tảng và mã hóa. Màn hình của dịch vụ này chỉ hiển thị tin nhắn của k người sau cùng. Khi có một tin nhắn được gởi đến bạn thì tin nhắn sẽ được hiển thị vào đầu danh sách tin nhắn. Các tin nhắn sẽ được nhóm lại theo số điện thoại (SĐT) của người gởi. Cho một chuỗi tuần tự các SĐT có gởi tin nhắn cho bạn:

2.1. Hãy mô tả cấu trúc dữ liệu (CTDL) sử dụng để hiển thị tin nhắn của k người sau cùng và các tin nhắn sẽ được nhóm lại theo SĐT của người gởi (xem mô tả ví dụ input, ouput bên dưới) (0.5 điểm)

2.2. Viết chương trình bằng C++ hiện thực hoá yêu cầu, sử dụng CTDL trong câu 2.1 (1.5 điểm)

Ví dụ Input:

• Dòng 1: Số k
• Dòng 2: Số n: số lượng tin nhắn được gởi đến bạn
• Dòng 3: Danh sách SĐT của n tin nhắn theo thứ tự thời gian từ trước đến sau

Lưu ý: Giới hạn SĐT chỉ có tối đa 3 chữ số

Ví dụ Output: Danh sách các SĐT của các tin nhắn hiển thị trên màn hình theo thứ tự SĐT có tin nhắn mới hơn sẽ xuất hiện trước kèm theo số lượng tin nhắn từ SĐT đó.

Input	Output
5 12 903 901 902 904 976 976 973 986 976 904 905 986	986(2) 905 904(2) 976(3) 973

Bài làm tham khảo

2.1. Cấu trúc dữ liệu được dùng để hiển thị tin nhắn của k người sau cùng là stack, các số điện thoại của các tin nhắn mới nhất sẽ ở trên đầu của stack, để hiển thị tin nhắn của k người, ta chỉ cần truy ngược lại theo stack đã lưu.

2.2. Đoạn code tham khảo:

#include <iostream>
#include <stack>

using namespace std;

int main() {
	int k, n;
	stack<int> sdt;
	int soLuongTinNhan[1000] = { 0 }; // Mảng để lưu số lượng tin nhắn của mỗi số điện thoại,
    // vì số điện thoại chỉ có 3 chữ số nên ta sẽ lưu mảng 1000 phần tử, có thể dùng bảng băm để lưu thay vì mảng

	cin >> k >> n;
	for (int i = 0; i < n; ++i) {
		int s; cin >> s;
		sdt.push(s);
		soLuongTinNhan[s]++;
	}

	for (int i = 0; i < k; ++i) {
		int s = sdt.top();
		sdt.pop();

		if (soLuongTinNhan[s] > 0) {
			cout << s;
			if (soLuongTinNhan[s] > 1)
				cout << "(" << soLuongTinNhan[s] << ")";
			cout << " ";
			soLuongTinNhan[s] = 0; // Đặt số lượng tin nhắn về 0 sau khi đã in ra để không bị in trùng
		}
		else
			--i; // Nếu số lượng tin nhắn là 0 mà nằm trong stack nghĩa là đã in ra rồi,
				// chúng ta sẽ không đếm
	}
}

Câu 3

3.1. Cho dãy ký tự như sau: I, S, G, L, X, V, A, T, E, R, H, Y, hãy vẽ cây nhị phân tìm kiếm khi thêm từng ký tự vào cây theo thứ tự từ trái qua phải của dãy ký tự, biết rằng giá trị của từng ký tự tương ứng theo thứ tự xuất hiện của ký tự trong từ điển như sau: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z (0.5 điểm)

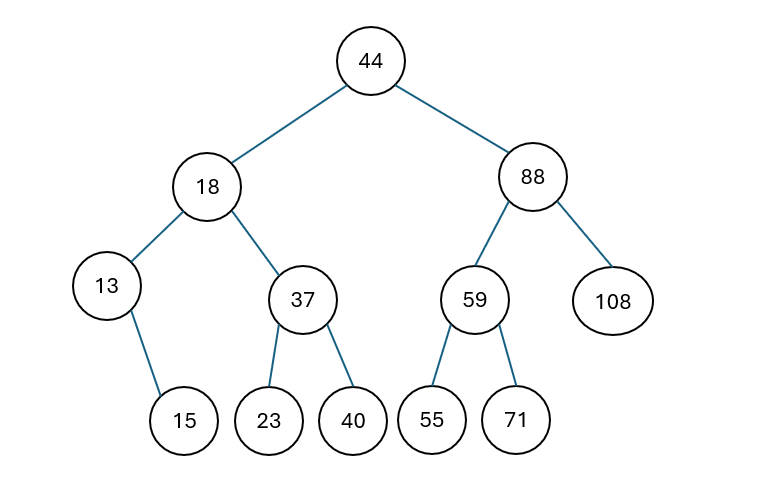
3.2. Cho biết kết quả duyệt cây nhị phân tìm kiếm (hình dưới) theo RNL, NRL (0.5 điểm)

3.3. Viết hàm đếm số nút có 2 nút con trên cây nhị phân tìm kiếm (0.5 điểm)

Bài làm tham khảo

3.1. Lần lượt chèn các kí tự vào cây nhị phân tìm kiếm, xét từng kí tự, nếu thứ tự từ điển lớn hơn node đang xét (bắt đầu từ node gốc), ta sẽ di chuyển về bên phải, nếu không ta sẽ di chuyển về bên trái, cho đến khi có trống để thêm node mới vào, kết quả cuối cùng sẽ như hình dưới.

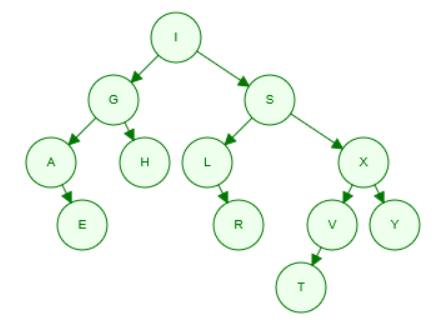
3.2.

• Kết quả của phép duyệt RNL: 108, 88, 71, 59, 55, 44, 40, 37, 23, 18, 15, 13.
• Kết quả của phép duyệt NRL: 44, 88, 108, 59, 71, 55, 18, 37, 40, 23, 13, 15.

3.3. Đoạn code tham khảo:

int count(TREE node)
{
	if (node != NULL) {

		int a = count(node->pLeft);
		int b = count(node->pRight);

		if (node->pLeft != NULL && node->pRight != NULL)
			return 1 + a + b;

		return a + b;
	}
	return 0;
}

Câu 4

Cho biết B-Tree bậc 5 là một cây đa nhánh thỏa mãn đồng thời tất cả các tính chất sau:

• Tất cả node lá phải nằm trên cùng một mức
• Tất cả các node, trừ node gốc và node lá có tối thiểu là 2 khóa và 3 con.
• Tất cả các node có tối đa là 4 khóa và 5 con
• Một node không phải là lá và có n khóa thì bắt buộc phải có n+1 con.

Lần lượt thêm các giá trị sau đây vào cây: 9, 8, 23, 2, 14, 17, 27, 11, 1, 24, 16, 5, 7, 13, 4, 18, 25, 19, 22, 26, 15, 29, 3.

4.1. Vẽ trạng thái của cây sau khi thêm toàn bộ các giá trị trên. (1 điểm)

4.2. Cho biết cấu trúc BTree_node và một hàm duyệt cây được định nghĩa như sau:

struct BTree_node {
	vector<int> keys;
	vector<BTree_node*>children;
};
void dfs2(BTree_node* root) {
	stack<BTree_node*> q;
	q.push(root);
	while(q.empty() != true) {
		BTree_node* x = q.top(); q.pop();
		for (int i : x->keys) cout << i << " ";
		cout << endl;
		for(BTree_node* i: x->children) q.push(i);
	}
}

Với cây B-Tree bậc 5 có hình dáng như bên dưới thì hàm duyệt cây trên sẽ cho ra output là gì? (0.5 điểm)

Bài làm tham khảo

4.1. Trạng thái cuối cùng của B-Tree

Các bạn có thể tham khảo chi tiết các bước vẽ tại đây.

4.2. Khi đọc đoạn code, ta thấy ngay đó là thuật toán duyệt theo chiều sâu của một cây, chỉ khác ở chỗ thay vì in 1 khóa của node đó như bình thường thì ở đây sẽ duyệt qua hết các khóa của 1 node rồi in ra, vì 1 node của B-Tree có nhiều khóa.

Vì vậy chúng ta chỉ cần duyệt cây theo chiều sâu như bình thường và viết kết quả. Lưu ý là các node con được đưa vào stack theo thứ tự nên khi duyệt, các node con sẽ được duyệt ngược lại.

Kết quả cuối cùng:

17
22 25
26 27 28 29
23 24
18 19 20 21
3 7 10 13
14 15 16
11 12
8 9
4 5 6
1 2

Câu 5

5.1. Cho bảng băm T có các đặc điểm sau:

• Kích thước bảng băm $m = 7$.
• Giá trị khóa $k$ là các số nguyên $k \in [1, 50]$.
• Sử dụng hàm băm theo phép chia.
• Xử lý đụng độ (hay va chạm, collision) theo phương pháp thăm dò tuyến tính.

Hãy cho biết công thức của hàm băm $h(k)$ và hàm băm lại $h_i(k)$, hay $h(k, i)$, sao cho xác suất xảy ra đụng độ trong T không vượt quá $n/m$ khi T có $n$ phần tử. (0.5 điểm).

5.2. Cho bảng băm T có các đặc điểm sau:

• Giá trị khóa k là một số nguyên dương.
• Kích thước bảng băm $m = 11$.
• Hàm băm $h(k) = floor(((0.618 * k) \mod 1) * m)$.
• Hàm băm lại $h(k, i) = floor(((0.618 * (k + i)) \mod 1) * m)$.

Cho biết :

• Hàm $floor(x)$ trả về giá trị nguyên lớn nhất nhỏ hơn hoặc bằng $x$. Ví dụ $floor(4.8) = 4$.
• Biểu thức $x \mod 1$ sẽ lấy phần thập phân của $x$. Ví dụ, $8.492 \mod 1 = 0.492$.
• Các số thực chỉ lấy đến ba số sau phần thập phân.

Giả sử bảng băm T đã chứa các khóa như sau:

Chỉ số	0	1	2	3	4	5	6	7	8	9	10
Khóa			2				9

Hãy trình bày quá trình:

a. Thêm khóa có giá trị 1 vào T. (0.5 điểm)

b. Giả sử khóa 2 đã bị xóa (ô có chỉ số 2 trên T chứa ký hiệu DELETED). Tìm khóa có giá trị 1 trên T. (0.5 điểm)

Bài làm tham khảo

5.1. Theo định lý họ hàm băm phổ quát thì hàm băm $h(k) = ((a*k + b) \mod p) \mod m$ sẽ có xác suất xảy ra đụng độ không vượt quá $n/m$ khi bảng băm có $n$ phần tử.

Trong đó: $a$ là số tự nhiên khác 0, $b$ là số tự nhiên, $p$ là số nguyên tố lớn hơn giá trị lớn nhất của $k$.

Ở đây, ta có thể chọn $a$, $b$, $p$ bất kì để tạo một hàm băm thỏa đề bài (lưu ý $p$ phải là số nguyên tố lớn hơn giá trị lớn nhất của $k$), ví dụ như: $h(k) = ((2 * k + 1) \mod 53) \mod 7$

Vì xử lý đụng độ theo phương pháp dò tuyến tính, hàm băm lại sẽ phải là: $h(k, i) = (h(k) + i) \mod 7$

5.2.

a.

• $h(1) = 6, T[6] = 9$ đụng độ $\rightarrow$ băm lại
• $h(1,1) = 2, T[2] = 2$ đụng độ $\rightarrow$ băm lại.
• $h(1,2) = 9, T[9]$ còn trống $\rightarrow$ gán $T[9] = 1$.

b.

• $h(1) = 6, T[6] = 9$ đụng độ $\rightarrow$ băm lại
• $h(1,1) = 2, T[2] =$ DELETED đụng độ $\rightarrow$ băm lại.
• $h(1,2) = 9, T[9] = 1$ $\rightarrow$ tìm thấy.

Câu 6

Bài toán tìm đường đi ngắn nhất giữa hai đỉnh trên đồ thị có thể được phát biểu dưới dạng tổng quát như sau: Cho một đơn đồ thị có hướng và có trọng số dương $G=(V,E)$, trong đó $V$ là tập đỉnh, $E$ là tập cạnh và các cạnh đều có trọng số, hãy tìm một đường đi ngắn nhất (không có đỉnh lặp lại) từ đỉnh xuất phát $s$ thuộc $V$ đến đỉnh đích $g$ thuộc $V$. Đường đi ngắn nhất giữa hai đỉnh có tổng các trọng số của các cạnh tạo nên đường đi đó là nhỏ nhất.

Giả sử thông tin đầu vào của bài toán (Input) được nhập vào chương trình và kết quả đầu ra (Output) bao gồm:

Input	Giải thích
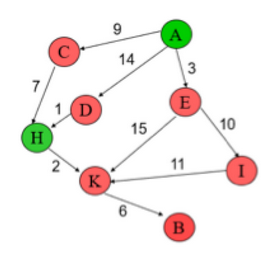
8 10 A B C D E H I K A C 9 A D 14 A E 3 C H 7 D H 1 E I 10 E K 15 H K 2 I K 11 K B 6 A K	- Dòng đầu tiên chứa 2 số nguyên dương v và e, lần lượt là số đỉnh và số cạnh của đồ thị. - Dòng tiếp theo chứa v chuỗi (chuỗi không có khoảng trắng) là danh sách tên các đỉnh. - Với $e$ dòng tiếp theo, mỗi dòng chứa hai chuổi $u, i$ và một số nguyên dương x, thể hiện thông tin có một cạnh nối từ đỉnh $u$ sang đỉnh $i$ trong đồ thị với độ dài (trọng số là x. - Dòng cuối cùng chứa hai chuỗi s và g, đây là đỉnh bắt đầu và đỉnh kết thúc của đường đi cần tìm Lưu ý: thông tin nhập tương ứng với đồ thị có hình như bên dưới
Output	Giải thích
A D H K	Danh sách các đỉnh trên đường đi (cả đỉnh xuất phát và đỉnh đích)

Hãy thực hiện các yêu cầu sau: 6.1. Xây dựng các CTDL phù hợp nhất có thể để biểu diễn đồ thị trên máy tính theo input đã cho (0.5 điểm).

Cấu trúc được xem là tốt nếu đạt được các tiêu chuẩn sau: Tiết kiệm tài nguyên; Hỗ trợ một số thao tác cơ bản như: "Kiểm tra hai đỉnh có kề nhau không", "Tìm danh sách các đỉnh kề với một đỉnh cho trước" với ràng buộc là không phải duyệt qua danh sách tất cả các cạnh của đồ thị.

6.2. Dưới đây là một ví dụ về mã giả của thuật toán Dijkstra để tìm một đường đi ngắn nhất từ đỉnh xuất phát s đến đỉnh đích g trong đồ thị. Hãy minh hoạ các bước thực hiện của thuật toán theo mã giả đã cho để "Tìm đường đi ngắn nhất từ đỉnh A đến đỉnh H" trong đồ thị bên dưới (0.75 điểm).

Gọi:

• open : tập các đỉnh có thể xem xét lựa chọn cho bước đi tiếp theo, các đỉnh có thể được xem xét lại, đỉnh chờ duyệt
• close : tập các đỉnh đã xét/đã duyệt, không xem xét lại
• s : đỉnh xuất phát
• g : đỉnh đích
• p : đỉnh đang xét, đỉnh hiện hành
• Hàm d(u) dùng để lưu trữ độ dài đường đi ngắn nhất từ đỉnh nguồn s đến đỉnh u
• w(u, i) : trọng số của cạnh nối từ đỉnh u tới đỉnh i
• parent(q) = p: lưu thông tin cha con, đỉnh p là cha của đỉnh q

Các bước thực hiện chính:

• Bước 1: Khởi tạo: open = {s} close = { } d(s) = 0

• Bước 2: while (open != {})

  2.1 Chọn p thuộc open có d(p) nhỏ nhất (xóa p ra khỏi open). Nếu có nhiều đỉnh cùng giá trị d(p) nhỏ nhất thì chọn đỉnh nhập vào sau trong danh sách đỉnh.

  2.2 Nếu p là đỉnh đích thì xuất đường đi, kết thúc thuật toán.

  2.3 Nếu p đã duyệt rồi thì bỏ qua, không xem xét lại, trở lại đầu vòng lặp

  2.4 Đánh dấu p đã duyệt qua rồi (tức thêm p vào close)

  2.5 Với mỗi đỉnh q kề với p, nếu q không thuộc close:

  2.5.1 Nếu q đã có trong open và d(q) > d(p) + w(p, q) thì cập nhật các thông tin: d(q) = d(p) + w(p, q) parent(q) = p

  2.5.2 Nếu q chưa có trong Open: d(q) = d(p) + w(p,q) parent(q) = p Thêm q vào open

• Bước 3: Kết luận “Không tìm thấy đường đi”.

6.3. Hãy thiết kế CTDL cho các đối tượng được đề cập trong thuật toán 6.2 (như open, close, hàm d(u), parent) và viết hoàn chỉnh hàm Dijkstra để giải quyết bài toán nêu trên (0.75 điểm).

Bài làm tham khảo

6.1. Cấu trúc dữ liệu biểu diễn đồ thị trên máy tính phù hợp là:

vector<vector<int>> matrix; // ma trận trọng số của đồ thị
vector<string> vNames; // Cấu trúc lưu danh sách các tên đỉnh
map<string, int> vIndices;

• matrix biểu diễn giá trị của mỗi ô trong ma trận nếu khác 0 thì cho biết trọng số của cạnh nối giữa 2 đỉnh tương ứng
• Do đỉnh có tên là chuỗi nên cần có cách ánh xạ từ chuỗi sang số nguyên (vIndices) cho biết index dòng/cột tương ứng trong ma trận

6.2.

p	open	close	parent
	(A, 0)
A	(C, 9), (D, 14), (E, 3)	A
E	(C, 9), (D, 14), (I, 13), (K, 18)	A, E	A
C	(D, 14), (I, 13), (K, 18), (H, 16)	A, E, C	A
I	(D, 14), (K, 18), (H, 16)	A, E, C, I	E
D	(K, 18), (H, 15)	A, E, C, I, D	A
H			D

6.3. Thuật toán Dijkstra dựa trên mã giả

void Dijkstra(string s, string g)
{
	priority_queue<int, string>, vector<pair<int, string>>, greater<pair<int, string>>> open;
	vector<bool> close(v, false);
	map<string, string> parent;
	vector<int> d(v, INT_MAX);

	open.push({0, s});
	while (!open.empty())
	{
		pair<int, string> top = open.top(); open.pop();
		string p = top.second;
		if (p == g)
		{
			FindPath(s, g);
			break;
		}
		if (close[index[p]])
			continue;
		close[index[p]] = true;

		for (int i = 0; i < v; ++i)
		{
			if (matrix[index[p]][i] > 0 && !close[i])
				if (d[i] > d[index[p]] + matrix[index[p]][i])
				{
					d[i] = d[index[p]] + matrix[index[p]][i];
					open.push({d[i], name[i]});
					parent[name[i]] = p;
				}
		}
	}
}