Chương 1: Giới thiệu về giải thuật
1. Khái quát về giải thuật
1.1. Định nghĩa
Giải thuật là một quy trình rõ ràng, được xác định và hiểu được để giải quyết một vấn đề tính toán. Để được coi là một giải thuật, một quy trình phải có ba tính chất sau:
- Tính chính xác: Các bước phải dẫn đến một kết quả đúng cho đầu vào hợp lệ.
- Tính hữu hạn: Giải thuật phải kết thúc sau một số bước hữu hạn.
- Tính khả thi: Giải thuật có thể áp dụng cho mọi trường hợp có đầu vào hợp lệ của bài toán.
Tóm lại: Giải thuật là một phương pháp hoặc quy trình giải quyết một vấn đề tính toán bằng cách mô tả một tập hữu hạn các bước đơn giản, mà sau khi thực hiện sẽ giải quyết vấn đề đó với đầu vào bất kỳ.
Ví dụ minh họa: Tính tổng các số từ 1 đến N
- Khởi tạo biến sum = 0
- Lặp từ 1 đến N, mỗi bước cộng số hiện tại vào sum
- Kết thúc và trả về sum
Phân biệt giải thuật và chương trình: Giải thuật là ý tưởng trừu tượng (công thức nấu ăn), còn chương trình là cách thực hiện hóa ý tưởng đó bằng ngôn ngữ lập trình (món ăn được nấu từ công thức).
1.2. Sự cần thiết của việc học giải thuật
- Giải thuật là cơ sở của khoa học máy tính
- Tối ưu hóa hiệu suất
- Giải quyết các vấn đề phức tạp
- Cải thiện khả năng logic và tư duy
- Sự cần thiết trong các lĩnh vực khác nhau
- Hiểu sâu về các cấu trúc dữ liệu
- Phát triển kỹ năng gỡ lỗi và phân tích
2. Phân tích thuật toán
- Dự đoán hiệu suất
- So sánh thuật toán
- Cung cấp đảm bảo
- Hiểu cơ sở lý thuyết
(?) Một số câu hỏi được đặt ra
- Liệu chương trình của tôi có thể giải quyết được một đầu vào thực tế lớn không?
- Tại sao chương trình của tôi lại chạy chậm?
- Tại sao chương trình của tôi lại hết bộ nhớ?
- Giải thuật nào tốt hơn trong các trường hợp cụ thể?
3. Độ phức tạp thuật toán
3.1. Một số khái niệm căn bản
- T(N) là hàm số để mô tả thời gian thực thi của một thuật toán, dựa trên kích thước đầu vào của nó.
- Big O là ký hiệu đại số để biểu diễn độ phức tạp thời gian của một thuật toán, biểu thị tốc độ tăng của hàm thời gian T(N) khi kích thước đầu vào N tiến đến vô hạn.
- Ký hiệu của Big O là "O", theo sau là một biểu thức đại số biểu thị hàm tốn thời gian của thuật toán, ví dụ như hoặc
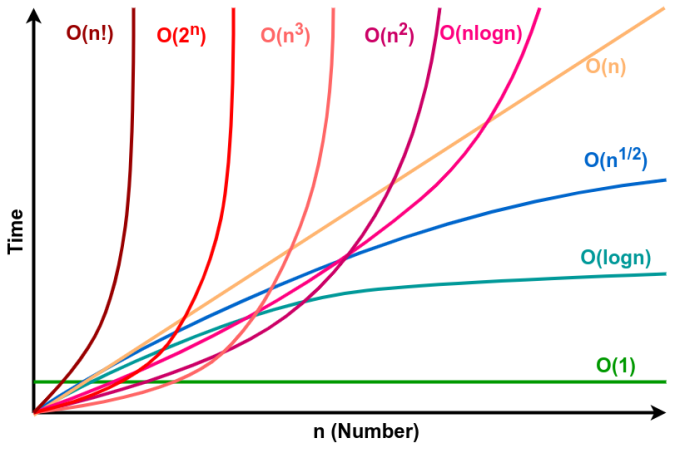
3.2. Một số độ phức tạp của giải thuật phổ biến
3.2.1. Tìm kiếm tuyến tính (Linear Search)
- Độ phức tạp tốt nhất là , khi phần tử cần tìm nằm ở vị trí đầu tiên.
- Độ phức tạp trung bình và xấu nhất là , phải duyệt qua toàn bộ danh sách.
3.2.2. Tìm kiếm nhị phân (Binary Search)
Điều kiện: Dữ liệu đầu vào cần được sắp xếp theo thứ tự tăng dần hoặc giảm dần.
- Độ phức tạp tốt nhất là , khi phần tử cần tìm nằm ở giữa danh sách.
- Độ phức tạp trung bình và xấu nhất là , mỗi bước loại bỏ một nửa dữ liệu.
3.2.3. Tìm kiếm nội suy (Interpolation Search)
Điều kiện: Dữ liệu đầu vào cần được sắp xếp theo thứ tự tăng dần hoặc giảm dần.
- Độ phức tạp tốt nhất là , khi dữ liệu được phân bố đều.
- Độ phức tạp trung bình và xấu nhất là , khi dữ liệu không được phân bố đều.
3.2.4. Thuật toán tìm kiếm tuyến tính cải tiến
Sử dụng phương pháp "skip" để tăng tốc độ tìm kiếm.
- Độ phức tạp tốt nhất là , khi phần tử nằm ở vị trí đầu tiên.
- Độ phức tạp trung bình là , trong đó là số phần tử bị "skip" qua.
- Độ phức tạp xấu nhất là .
3.2.5. Độ phức tạp của một số giải thuật sắp xếp
- Sắp xếp nổi bọt (Bubble Sort):
- Sắp xếp chọn (Selection Sort):
- Sắp xếp chèn (Insertion Sort):
- Sắp xếp nhanh (Quick Sort):
- Sắp xếp trộn (Merge Sort):
- Sắp xếp vun đống (Heap Sort):
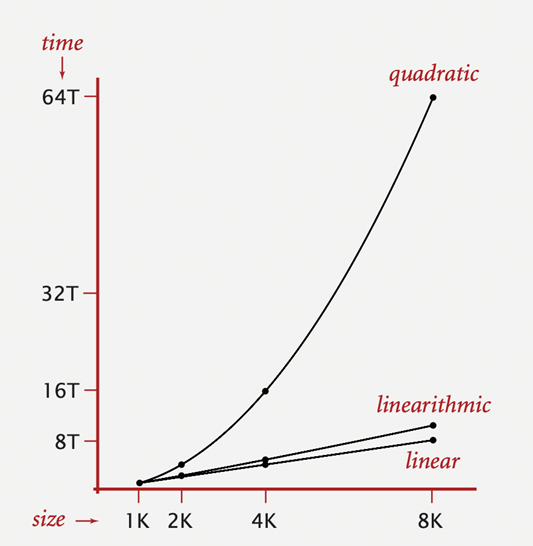
Bài tập
3.3. Phát triển Câu 1a Đề minh họa Cuối kỳ DSA
Câu 1:
a) Hãy cho biết độ phức tạp của thuật toán Heap sort theo định nghĩa Big-O (0.25đ)
b) Hãy cho biết độ phức tạp của thuật toán Quick sort theo định nghĩa Big-O (0.25đ)
c) Hãy cho biết độ phức tạp của thuật toán Insertion sort theo định nghĩa Big-O (0.25đ)
d) Hãy cho biết độ phức tạp của thuật toán Selection sort theo định nghĩa Big-O (0.25đ)
e) Hãy cho biết độ phức tạp của thuật toán Merge sort theo định nghĩa Big-O (0.25đ)
f) Hãy cho biết độ phức tạp của thuật toán Tìm kiếm tuyến tính (Linear Search) theo định nghĩa Big-O (0.25đ)
g) Hãy cho biết độ phức tạp của thuật toán Tìm kiếm nhị phân (Binary Search) theo định nghĩa Big-O (0.25đ)