Chương 3. Các thuật toán sắp xếp
1. Sắp xếp chọn (Selection Sort)
1.1. Sơ lược về nguồn gốc
Selection Sort là một thuật toán sắp xếp đơn giản và dễ triển khai, hoạt động dựa trên nguyên tắc chọn phần tử nhỏ nhất trong đoạn chưa được sắp xếp và hoán đổi nó với phần tử đầu tiên của đoạn đó. Quá trình này được lặp lại cho đến khi toàn bộ mảng được sắp xếp. Selection Sort được phát triển và nghiên cứu bởi John von Neumann vào năm 1945, sau đó được chuẩn hoá lại bởi Robert W. Floyd vào năm 1964. Mặc dù không phải là thuật toán tối ưu về mặt hiệu năng. Selection Sort vẫn được xem là một ví dụ kinh điển giúp người học nắm rõ các khái niệm cơ bản về sắp xếp, vòng lặp lồng nhau và thao tác với mảng.
1.2. Ý tưởng
Selection Sort chia mảng thành hai phần: phần đã sắp xếp (bên trái) và phần chưa sắp xếp (bên phải). Ban đầu, phần sắp xếp rỗng và phần chưa sắp xếp là toàn bộ mảng. Ý tưởng thuật toán như sau:
- Tìm phần tử nhỏ nhất trong phần chưa sắp xếp.
- Đặt phần tử nhỏ nhất này vào vị trí đầu tiên của phần chưa sắp xếp (tức là vị trí tiếp theo của phần đã sắp xếp).
- Tiếp tục quá trình này cho đến khi toàn bộ mảng được sắp xếp.
1.3. Pseudocode:
- Bước 1: Gán
i = 0 - Bước 2: Tìm chỉ số
mincủa phần tử nhỏ nhất trong đoạn từa[i]đếna[n - 1] - Bước 3: Hoán vị
a[min]vàa[i] - Bước 4: Nếu
i<n - 1thìi = i + 1và quay lại bươc 2. Ngược lại, kết thúc.
1.4. Cài đặt hàm
void selectionSort(int arr[], int n) {
int i, j, min_idx;
for (i = 0; i < n - 1; i++) {
min_idx = i;
for (j = i + 1; i < n; j++) {
if (arr[j] < arr[min_idx]) {
min_idx = j;
}
swap(arr[min_idx], arr[i]);
}
}
}
Trong đó:
arrlà mảng chứa các phần tử cần sắp xếp.nlà số lượng phần tử trong mảng.ilà biến lặp bên ngoài, duyệt từ đầu đến cuối mảng để tìm vị trí phần tử đang xét.jlà biến lặp bên trong, duyệt từ vị tríi + 1đến cuối mảng để tìm phần tử nhỏ nhất trong phần còn lại của mảng.min_idxlà biến lưu vị trí của phần tử nhỏ nhất trong phần còn lại của mảng.- Hàm
swap()là hàm trao đổi giá trị của hai biến.
1.5. Biểu diễn chi tiết thuật toán
1.6. Ví dụ
Sắp xếp mảng một chiều a gồm có các phần tử: 3, 1, 2, 7, 5.
- Khởi tạo mảng:
i = 0,a[i] = 3
min_idx = 1,a[min_idx] = 1
swap(a[i], a[min_idx]) ta được phần tử i = 0 đã được sắp xếp
- Bước tiếp theo,
i = 1,a[i] = 3
min_idx = 2,a[min_idx] = 2swap(a[i], a[min_idx])ta được phần tửi = 1đã được sắp xếp
- Bước tiếp theo,
i = 2,a[i] = 3
min_idx = 2,a[min_idx] = 3swap(a[i]m, a[min_idx])ta được phần tửi = 2đã được sắp xếp
- Bước tiếp theo,
i = 3,a[i] = 7
min_idx = 4,a[min_idx] = 5swap(a[i], a[min_idx])ta được phần tửi = 3đã được sắp xếp
- Kết thúc chương trình, ta được mảng đã sắp xếp.
1.7. Bài tập luyện tập
BT 1.7.1. Sắp xếp mảng số nguyên tăng dần, giảm dần
BT 1.7.2. Sắp xếp mảng số thực tăng dần, giảm dần
BT 1.7.3. Sắp xếp mảng phân số tăng dần, giảm dần
BT 1.7.4. Sắp xếp mảng tăng dần, giảm dần và đếm số lần truy cập vào các phần tử
2. Sắp xếp chèn (Insertion Sort)
2.1. Giới thiệu
- Insertion Sort là một thuật toán sắp xếp đơn giản và hiệu quả khi áp dụng cho một lượng nhỏ các phần tử.
- Một ví dụ minh họa trong thực tế là khi chơi bài tây. Mỗi khi bạn bốc một lá bài và xếp nó vào tay, bạn đang vô tình áp dụng thuật toán Insertion Sort để sắp xếp các lá bài theo thứ tự nào đó.
2.2. Mô tả cách hoạt động của thuật toán Insertion Sort bằng việc xếp các lá bài
Bước 1: Bắt đầu với một tay trống và các lá bài úp mặt xuống trên bàn.
Bước 2: Lấy từng lá bài từ bàn và xem nó như một phần tử cần được sắp xếp.
Bước 3: Chèn nó vào vị trí đúng trong tay trái.
Để tìm vị trí đúng cho một lá bài, chúng ta so sánh nó với mỗi lá bài đã có trong tay trái, từ phải sang trái.
Luôn luôn, các lá bài nằm trong tay trái đã được sắp xếp.
Bước 4: Lặp lại các bước 2 đến 3 cho đến khi tất cả các lá bài được chèn vào tay.
Tương tự, thuật toán Insertion Sort sẽ sắp xếp các phần tử trong một mảng theo thứ tự tăng dần bằng cách chèn từng phần tử vào đúng vị trí đúng của nó trong mảng đã được sắp xếp trước đó.
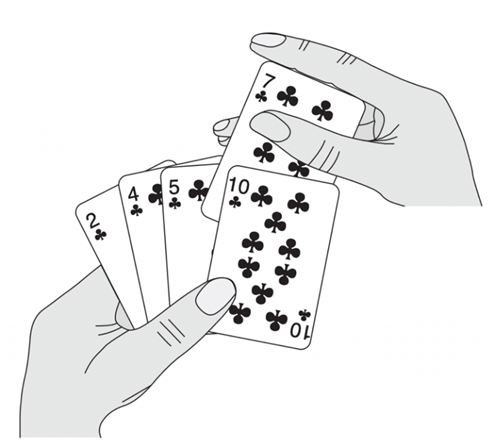
2.3. Ví dụ minh họa
A = {7, 10, 5, 3, 8, 4, 2, 9, 6} và n = 9
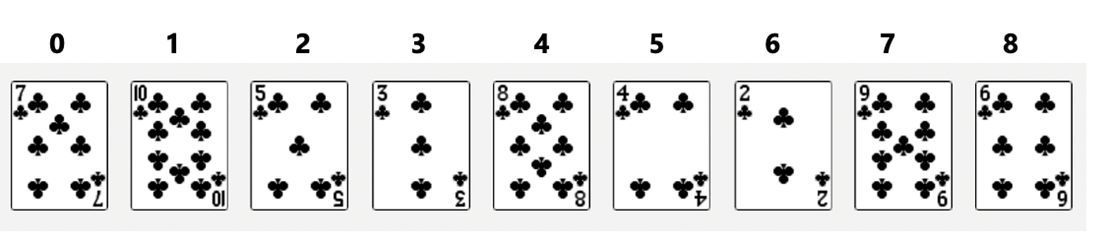 Bước 1: Chèn
Bước 1: Chèn A[1] = 10 vào đoạn [0, 0] sao cho ta được đoạn [0, 1] có thứ tự


Bước 2: Chèn A[1] = 5 vào đoạn [0, 1] sao cho ta được đoạn [0, 2] có thứ tự


Bước 3: Chèn A[3] = 3 vào đoạn [0, 2] sao cho ta được đoạn [0, 3] có thứ tự


Bước 4: Chèn A[4] = 8 vào đoạn [0, 3] sao cho ta được đoạn [0, 4] có thứ tự


Bước 5: Chèn A[5] = 4 vào đoạn [0, 4] sao cho ta được đoạn [0, 5] có thứ tự


Bước 6: Chèn A[6] = 2 vào đoạn [0, 5] sao cho ta được đoạn [0, 6] có thứ tự


Bước 7: Chèn A[7] = 9 vào đoạn [0, 6] sao cho ta được đoạn [0, 7] có thứ tự


Bước 8: Chèn A[8] = 6 vào đoạn [0, 7] sao cho ta được đoạn [0, 8] có thứ tự

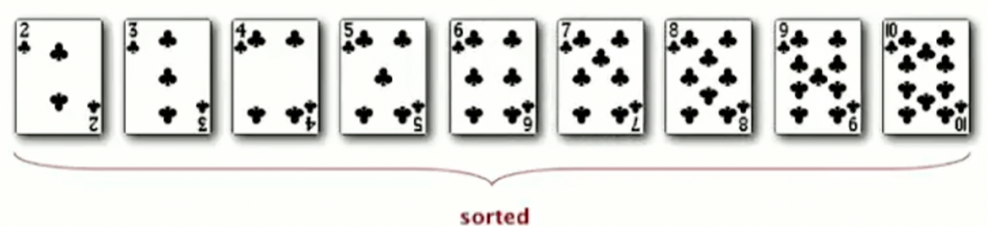
- Kết thúc giải thuật, dãy số kết quả là: 2 3 4 5 6 7 8 9 10
2.4. Đoạn code c++ cho thuật toán Insertion Sort
void insertionSort(int arr[], int n) {
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
2.5. Insertion Sort: animation
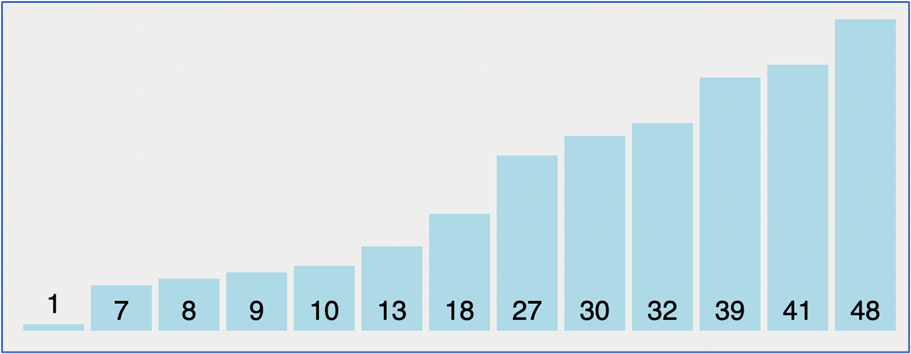
- Web tham khảo chạy từng bước thuật toán: https://visualgo.net/en/sorting
3. Sắp xếp nổi bọt (Bubble Sort)
- Bubble Sort, hay còn gọi là sắp xếp nổi bọt, là một thuật toán sắp xếp đơn giản và cổ điển. Thuật toán này được gọi là nổi bọt vì các phần tử lớn nhất sẽ dần nổi lên cuối mảng sau mỗi vòng lặp, giống như bọt khí nổi lên mặt nước.
- Được phát triển vào những năm 1950, thuật toán này đã trở thành một phần quan trọng trong việc giảng dạy các thuật toán sắp xếp cơ bản trong lĩnh vực khoa học máy tính.

3.1. Mô tả cách hoạt động của thuật toán Bubble Sort
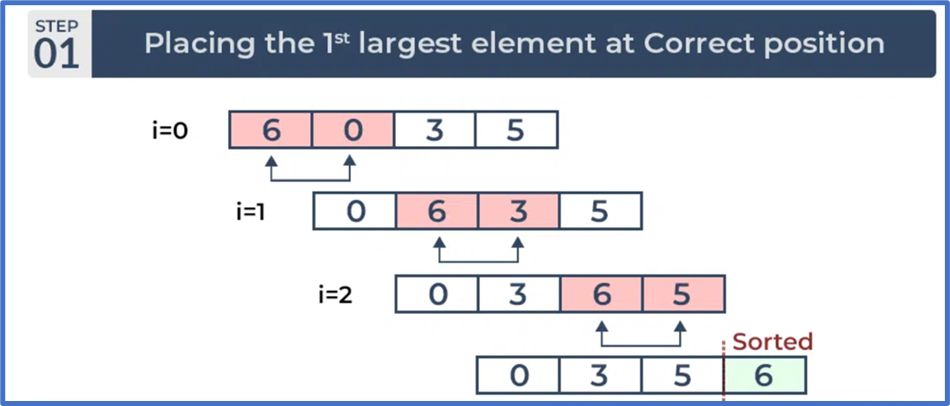
- Input:
arr[] = {6, 3, 0, 5}
Bước 1: Vòng lặp thứ nhất:
Phần tử lớn nhất được đặt ở vị trí chính xác của nó, tức là ở cuối mảng.
 Bước 2: Lần lặp thứ hai:
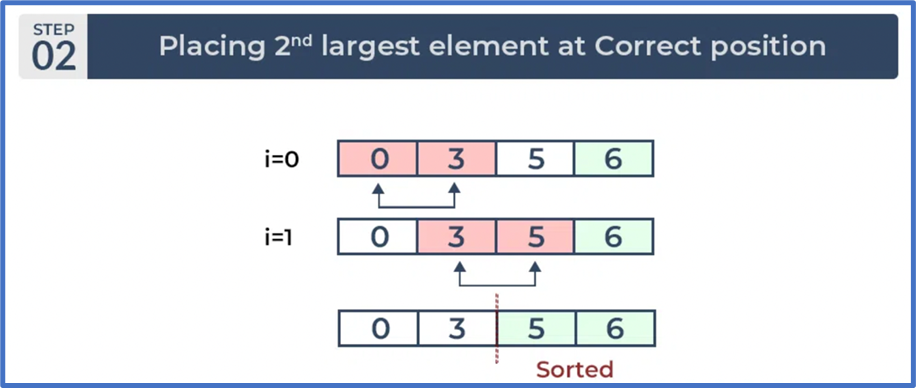
Bước 2: Lần lặp thứ hai:
Đặt phần tử lớn thứ hai ở vị trí đúng.
 Bước 3: Lần lặp thứ ba:
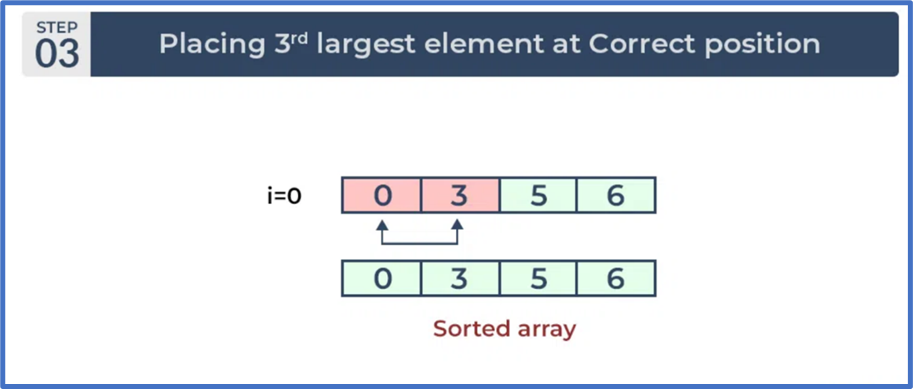
Bước 3: Lần lặp thứ ba:
Đặt hai phần tử còn lại ở vị trí đúng của chúng.
3.2. Đoạn code c++ cho thuật toán Bubble Sort
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
}
}
4. Sắp xếp nhanh (Quick Sort)
4.1. Sơ lược về nguồn gốc
- Quick sort là một thuật toán sắp xếp được phát minh bởi nhà khoa học máy tính người Anh Tony Hoare vào năm 1959 khi ông đang làm việc tại câu lạc bộ Turing ở Luân Đôn.
- Thuật toán này được coi là một trong những thuật toán sắp xếp nhanh nhất và được sử dụng rộng rãi trong thực tế.
4.2. Ý tưởng
- Ý tưởng chính của thuật toán Quick Sort là dựa trên thuật toán Chia để trị, chọn một phần tử làm trục (pivot) và phân vùng mảng đã cho xung quanh trục đã chọn bằng cách đặt trục vào đúng vị trí của nó trong mảng được sắp xếp.
- Thuật toán Quick Sort hoạt động bằng cách chọn một phần tử trong dãy đầu vào làm "pivot". Sau đó, các phần tử trong dãy đầu vào được phân thành hai phần: các phần tử nhỏ hơn hoặc bằng pivot được đưa về phía trước của pivot và các phần tử lớn hơn pivot được đưa về phía sau của pivot. Sau khi phân hoạch này được thực hiện, pivot sẽ được đặt vào giữa hai phần được phân chia.
- Sau đó, thuật toán sẽ đệ quy áp dụng phương pháp trên cho các phần tử nằm bên trái và phải của pivot cho đến khi dãy được sắp xếp hoàn toàn. Quá trình đệ quy sẽ kết thúc khi chỉ còn một phần tử hoặc không còn phần tử nào để phân chia.
- (!) Với mỗi đệ quy, thuật toán Quick Sort sẽ có thể chọn một pivot khác nhau. Có nhiều cách để chọn pivot, một cách đơn giản là chọn phần tử ở giữa dãy đầu vào. Tuy nhiên, sử dụng cách chọn pivot khác nhau sẽ ảnh hưởng đến hiệu suất của thuật toán Quick Sort.
4.3. Cài đặt hàm
- Chúng ta cần xác định được các hàm để thực hiện thuật toán Quick Sort:
- Hàm Quick Sort với 2 đối số (để sử dụng).
- Hàm Quick Sort với 3 đối số (phục vụ cho cài đặt hàm).
- Định nghĩa hàm:
- Quick Sort với 2 đối số:
void quickSort(int a[], int n) {
quickSort(a, 0, n - 1);
}- Quick Sort với 3 đối số:
void quickSort(int a[], int left, int right) {
if (left < right) {
int id_pivot = Partition(a, left, right);
quickSort(a, left, id_pivot - 1);
quickSort(a, id_pivot + 1, right);
}
}- Partition: Hàm partition có chức năng chia một mảng thành hai phần, một phần có giá trị nhỏ hơn hoặc bằng pivot (giá trị được chọn để so sánh và phân chia mảng) và một phần có giá trị lớn hơn pivot.
int partition(int a[], int left, int right) {
int pivot = a[right];
int id = left - 1;
for (int i = left; i < right; i++) {
if (a[i] <= pivot) {
id++;
swap(a[id], a[i]);
}
}
id++;
swap(a[id], a[right]);
return id;
}
4.4. Biểu diễn chi tiết thuật toán
Cho mảng gồm các phần tử {10, 5, 30, 70, 40, 80, 90} trình bày từng bước giải thuật Quick Sort để sắp xếp mảng giảm:
- Mảng ban đầu:
- Phân hoạch lần 1: (chọn 70 làm phần tử phân hoạch)
-
- Phân hoạch lần 2: (chọn 80 làm phần tử phân hoạch [đoạn 90, 80])
- Phân hoạch lần 3: (chọn 5 làm phần tử phân hoạch [đoạn 30, 40, 5, 10])
- Phân hoạch lần 4: Chọn phần tử 40 làm phần tử phân hoạch [đoạn 30, 40, 10]
- Kết thúc phân hoạch ta được mảng đã sắp giảm 5
4.5. Đánh giá thuật toán
4.5.1. Độ phức tạp
- Trung bình:
- Tốt nhất: (khi mảng được chia đều)
- Xấu nhất: (khi mảng đã sắp xếp hoặc đảo ngược)
4.5.2. Ưu điểm
- Quick Sort là một trong những thuật toán sắp xếp nhanh nhất.
- Quick Sort dễ dàng được cài đặt và tối ưu hóa.
- Quick Sort hoạt động hiệu quả trên bộ nhớ do không cần phải sử dụng thêm bộ nhớ phụ.
4.5.3. Nhược điểm
- Quick Sort có thể trở nên chậm nếu mảng đã được sắp xếp hoặc đảo ngược.
- Trong trường hợp xấu nhất, khi mảng đã được sắp xếp hoặc đảo ngược, Quick Sort có thể làm việc với độ phức tạp .
- Quick Sort không ổn định, nghĩa là vị trí tương đối của các phần tử bằng nhau có thể bị thay đổi sau khi được sắp xếp.
4.6. Bài tập luyện tập
- Sắp xếp một mảng số nguyên tăng dần bằng thuật toán Quick Sort.
- Sắp xếp một mảng số nguyên giảm dần bằng thuật toán Quick Sort.
- Sắp xếp một mảng số nguyên có phần tử trùng lặp bằng thuật toán Quick Sort.
- Sắp xếp một mảng số thực bằng thuật toán Quick Sort.
- Sắp xếp một mảng số nguyên theo thứ tự từ xa đến gần với một giá trị xác định bằng thuật toán Quick Sort.
- Sắp xếp một mảng số nguyên theo thứ tự từ gần đến xa với một giá trị xác định bằng thuật toán Quick Sort.
- Sắp xếp một mảng số nguyên bằng thuật toán Quick Sort sử dụng phương pháp "Hoare partition".
- Sắp xếp một mảng số nguyên bằng thuật toán Quick Sort sử dụng phương pháp "Lomuto partition".
- Sắp xếp một danh sách liên kết đơn có chứa các số nguyên bằng thuật toán Quick Sort.
5. Sắp xếp trộn (Merge Sort)
5.1. Sơ lược về nguồn gốc
- Merge Sort là một thuật toán sắp xếp đệ quy được phát minh bởi nhà khoa học máy tính John von Neumann vào năm 1945. Thuật toán Merge Sort được xây dựng trên nguyên tắc "chia để trị" (divide and conquer) và được thiết kế để giải quyết các vấn đề sắp xếp dữ liệu trên máy tính.
- Ban đầu, thuật toán Merge Sort được sử dụng để giải quyết vấn đề sắp xếp các bộ dữ liệu trên đĩa từ trong các máy tính đầu tiên. Sau đó, nó được ứng dụng rộng rãi trong các lĩnh vực khác như kinh doanh, khoa học, công nghệ và các lĩnh vực khác.
- Vì tính hiệu quả của nó, Merge Sort là một trong những thuật toán sắp xếp phổ biến nhất trong lĩnh vực khoa học máy tính và được sử dụng trong nhiều ứng dụng khác nhau.
5.2. Ý tưởng
- Ý tưởng chính của thuật toán Merge Sort là chia một danh sách cần sắp xếp thành các danh sách con nhỏ hơn, rồi sắp xếp từng danh sách con đó và sau đó trộn các danh sách con đã sắp xếp lại với nhau cho đến khi nhận được danh sách ban đầu đã sắp xếp.
- Thuật toán Merge Sort được thực hiện theo các bước sau:
- Chia danh sách cần sắp xếp thành các danh sách con độc lập. Điều này được thực hiện bằng cách chia đôi danh sách ban đầu và tiếp tục chia đôi cho đến khi chỉ còn một phần tử trong mỗi danh sách con.
- Sắp xếp các danh sách con này bằng cách sử dụng đệ quy. Tức là tiếp tục chia danh sách con đó thành các danh sách con nhỏ hơn và sắp xếp chúng cho đến khi chỉ còn một phần tử trong mỗi danh sách con.
- Trộn các danh sách con đã sắp xếp lại với nhau để tạo ra danh sách lớn hơn, được sắp xếp đúng thứ tự. Quá trình trộn này được thực hiện bằng cách so sánh phần tử đầu tiên của mỗi danh sách con và chọn phần tử nhỏ hơn để đưa vào danh sách kết quả. Tiếp tục thực hiện cho đến khi một trong hai danh sách con đã được trộn hết.
- Trả về danh sách đã được sắp xếp.
5.3. Cài đặt hàm
- Chúng ta cần xác định được các hàm để thực hiện thuật toán Merge Sort:
- Hàm Merge Sort với 2 đối số.
- Hàm Merge Sort với 3 đối số.
- Hàm Merge (để trộn các danh sách lại với nhau).
- Định nghĩa hàm:
- Merge Sort với 2 đối số:
void mergeSort(int a[], int n) {
mergeSort(a, 0, n - 1);
}- Merge Sort với 3 đối số:
void mergeSort(int a[], int left, int right)
{
if (left < right)
{
int mid = (left + right) / 2;
mergeSort(a, left, mid);
mergeSort(a, mid + 1, right);
merge(a, left, mid, right);
}
}- Merge:
void merge(int a[], int left, int mid, int right)
{
int m = left;
int n = mid + 1;
int k = 0;
int* temp = new int[right - left + 1];
while (!((m > mid) && (n > right)))
{
if ((a[m] < a[n] && m <= mid && n <= right) || (n > right))
temp[k++] = a[m++];
else
temp[k++] = a[n++];
}
for (int i = 0; i < k; i++)
a[left + i] = temp[i];
delete[] temp;
} - Trong đó:
left,mid,right: là các chỉ số của phần tử bên trái, giữa, bên phải mảng cần được sắp xếpm: là biến chạy trên mảng con thứ nhấtn: là biến chạy trên mảng con thứ haitemp: là mảng tạm thời để lưu trữ các phần tử
5.4. Biểu diễn chi tiết thuật toán
- Ví dụ: Cho mảng
a = {40, 20, 10, 4, 1, 19, 7}
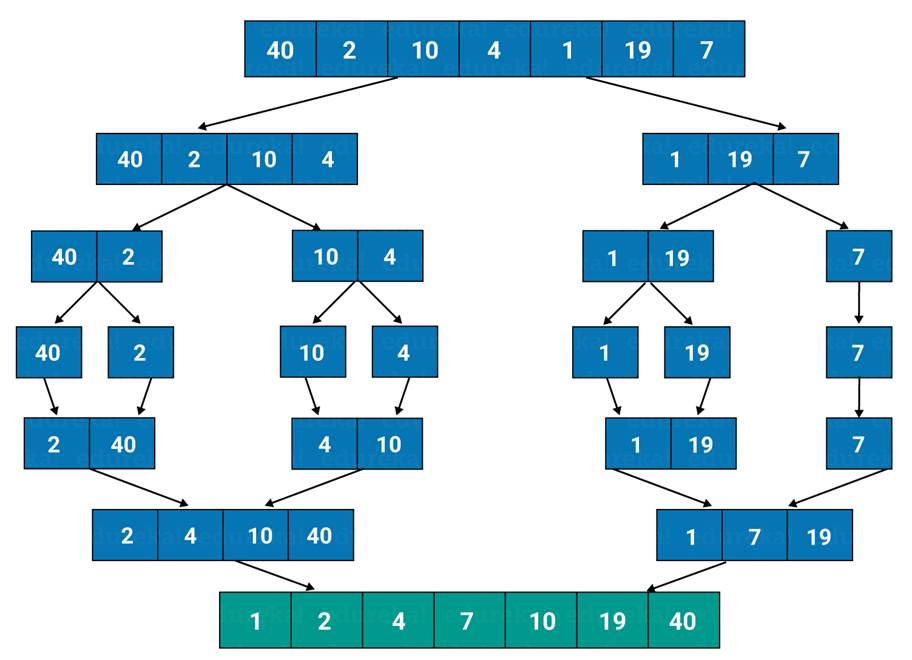
5.5. Đánh giá thuật toán
5.5.1. Độ phức tạp
Mọi trường hợp:
5.5.2. Ưu điểm
- Merge Sort là một thuật toán ổn định, nghĩa là nó không đổi vị trí các phần tử bằng nhau trong mảng đầu vào.
- Merge Sort có thể được thực hiện trên các dữ liệu liên tục, bởi vì việc chia mảng thành các mảng con không cần phải dùng đến con trỏ hoặc thêm bộ nhớ phụ.
- Merge Sort rất hiệu quả trong việc sắp xếp các danh sách liên kết, vì nó không cần truy cập phần tử bất kỳ đâu trong danh sách cho đến khi nó được sắp xếp.
5.5.3. Nhược điểm
- Merge Sort sử dụng một mảng phụ để lưu trữ các giá trị đã được sắp xếp, do đó nó cần thêm không gian bộ nhớ để lưu trữ các mảng con và mảng phụ này.
- Merge Sort yêu cầu một số lượng lớn các thao tác so sánh, điều này có thể khiến nó chậm hơn các thuật toán sắp xếp nhanh hơn như Quick Sort.
- Merge Sort không hiệu quả với dữ liệu nhỏ, vì chi phí của việc chia và ghép dữ liệu có thể vượt quá chi phí của việc sắp xếp các phần tử đó trực tiếp.
5.6. Bài tập luyện tập
- Sắp xếp một mảng số nguyên tăng dần bằng thuật toán Merge Sort.
- Sắp xếp một mảng số nguyên giảm dần bằng thuật toán Merge Sort.
- Sắp xếp một mảng số nguyên có phần tử trùng lặp bằng thuật toán Merge Sort.
- Sắp xếp một mảng số thực bằng thuật toán Merge Sort.
- Sắp xếp một mảng số nguyên theo thứ tự từ xa đến gần với một giá trị xác định bằng thuật toán Merge Sort.
- Sắp xếp một mảng số nguyên theo thứ tự từ gần đến xa với một giá trị xác định bằng thuật toán Merge Sort.
- Sắp xếp một danh sách liên kết đơn có chứa các số nguyên bằng thuật toán Merge Sort.
- Sắp xếp một danh sách liên kết đôi có chứa các số nguyên bằng thuật toán Merge Sort.
6. Sắp xếp vun đống (Heap Sort)
6.1. Sơ lược về lịch sử hình thành
Heap Sort được đề xuất bởi J.W.J.Williams năm 1981, thuật toán không những đóng góp một phương pháp sắp xếp hiệu quả mà còn xây dựng một cấu trúc dữ liệu quan trọng để biểu diễn hàng đợi có độ ưu tiên: Cấu trúc dữ liệu Heap.
6.2. Cấu trúc dữ liệu Binary Heap
-
Complete binary tree (Cây nhị phân đầy đủ)
Cây nhị phân (Binary tree) là một cấu trúc dữ liệu dạng cây. Trong đó mỗi nút (node) có tối đa hai nút con: nút con bên trái (left child) và nút con bên phải (right child). Nếu cây rỗng, nó không có nút nào.
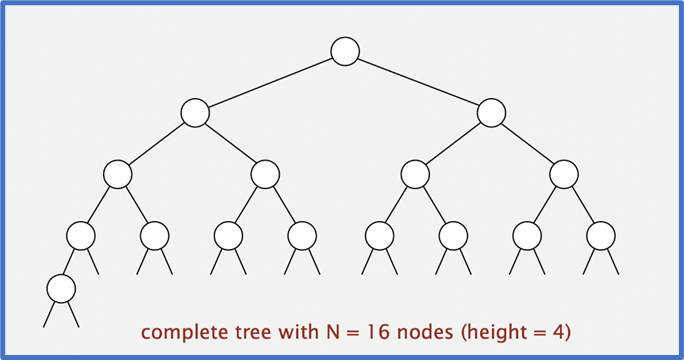
- Cây nhị phân đầy đủ (Complete binary tree): là một cây nhị phân mà tất cả các mức, trừ mức cuối cùng, đều có đầy đủ nút, và các nút ở mức cuối cùng được điền từ trái sang phải.
- Thuộc tính: Chiều cao của cây nhị phân đầy đủ có N nút là
- Chứng minh: Chiều cao chỉ tăng lên khi N là một lũy thừa của 2.
6.3. Thao tác Heapify
void heapify(int arr[], int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
}
- Giải thích ý nghĩa từng câu lệnh:
Bước 1: Hàm heapify được khai báo với ba đối số: một mảng số nguyên arr, kích thước của mảng n, và chỉ số i của nút gốc cần heapify:
void heapify(int arr[], int n, int i)
Bước 2: Một biến largest được khởi tạo với giá trị bằng chỉ số i, đại diện cho nút có giá trị lớn nhất trong ba nút gốc và hai nút con của nó.
int largest = i;
Bước 3: Hai biến left và right được khởi tạo để lưu chỉ số của hai nút con của nút gốc đang xét. Biểu thức 2 * i + 1 và 2 * i + 2 tính toán chỉ số của hai nút con trong mảng dựa trên chỉ số của nút gốc i.
int left = 2 * i + 1;
int right = 2 * i + 2;
Bước 4: Nếu chỉ số của nút con trái (left) nhỏ hơn kích thước của mảng và giá trị của nút con trái lớn hơn giá trị của nút có giá trị lớn nhất (largest), thì largest được cập nhật thành chỉ số của nút con trái.
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
Bước 5: Tương tự bước 4
if (right < n && arr[right] > arr[largest]){
largest = right;
}
Bước 6: Nếu chỉ số của nút lớn nhất (largest) khác với chỉ số của nút gốc ban đầu (i), tức là giá trị nút con lớn hơn giá trị nút gốc, thì hoán đổi giá trị nút gốc và nút lớn nhất, sau đó đệ quy hàm heapify cho nút con có giá trị lớn nhất.
if (largest != i) {
swap(arr[i], arr[largest]);
heapify(arr, n, largest);
}
Lưu ý: Để xây dựng hàm Heap ta gọi hàm heapify với mọi nốt không phải là nốt lá:
for (int i = (n/2)-1; i >= 0; i--) {
heapify(arr, n, i);
}
6.4. Cài đặt thuật toán Heap Sort
void heapSort(int arr[], int n) {
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
for (int i = n - 1; i >= 0; i--) {
swap(arr[0], arr[i]);
heapify(arr, i, 0);
}
}