Chuyển tới nội dung chính

Chương 6: Hàng đợi (Queue)

6.1. Sơ lược về hàng đợi​

6.1.1. Sơ lược về lịch sử hình thành:​

  • Khái niệm về hàng đợi đã tồn tại từ rất lâu trong cuộc sống hàng ngày trước khi nó được áp dụng vào lĩnh vực khoa học máy tính. Tuy nhiên, việc formalize và áp dụng hàng đợi vào lĩnh vực khoa học máy tính bắt đầu từ những năm 1940 và 1950.
  • Trong lĩnh vực toán học, một số nhà toán học đã nghiên cứu về hàng đợi trong thế kỷ 19, bao gồm Agner Krarup Erlang, người đã nghiên cứu về xếp hàng trong lĩnh vực lưu lượng cuộc gọi điện thoại.
  • Trong khoa học máy tính, hàng đợi được phát triển để giải quyết các vấn đề liên quan đến việc quản lý và tổ chức dữ liệu. Vào những năm 1950, hàng đợi đã trở thành một khái niệm quan trọng trong lĩnh vực lập trình và tính toán.
  • Ngôn ngữ lập trình FORTRAN, được phát triển bởi IBM vào những năm 1950, đã cung cấp các phương pháp để triển khai hàng đợi trong chương trình. Điều này đã tạo điều kiện thuận lợi cho việc phát triển và sử dụng hàng đợi trong các ứng dụng tính toán.

6.1.2. Khái niệm hàng đợi​

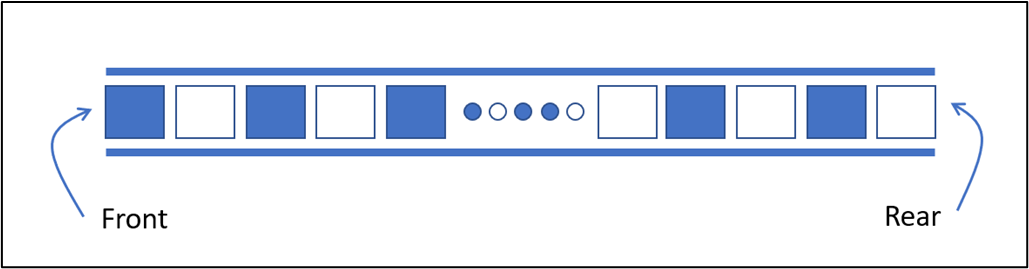
  • Hàng đợi là cấu trúc dữ liệu tuyến tính mở ở cả hai đầu và các thao tác được thực hiện theo thứ tự First In First Out (FIFO – Vào Trước Ra Trước) nghĩa là phần tử nào được đẩy vào hàng đợi đầu tiên thì các thao tác của hàng đợi sẽ thực hiện với phần tử đó đầu tiên

6.2. Khởi tạo​

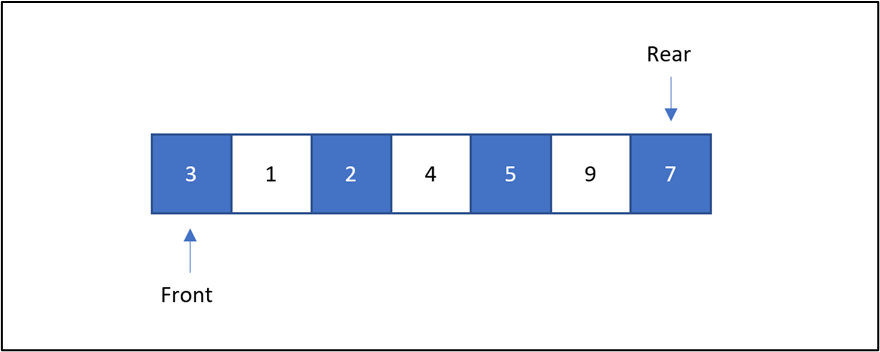
6.2.1. Khởi tạo queue trên mảng (array):​

typedef struct queue {
	char a[MAX];
	int front; //chỉ số của phần tử đầu trong Queue
	int rear; //chỉ số của phần tử cuối trong Queue
} QUEUE;

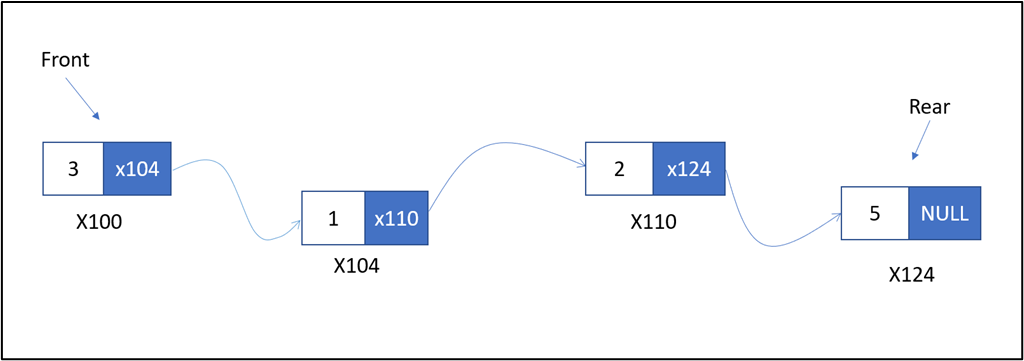
6.2.2. Khởi tạo queue trên danh sách liên kết đơn (singly linked-list):​

// Cấu trúc của một node
struct Node {
	int data;
	Node* next;
};
// Cấu trúc của một DSLK
struct QUEUE {
	Node* Front;
	Node* Rear;
};

6.3. Ứng dụng của Queue​

6.3.1. Trong các thuật toán:​

  • Quay lui (Backtracking): Trong thuật toán quay lui, queue có thể được sử dụng để lưu trữ các trạng thái tạm thời hoặc các lựa chọn tiếp theo để thử.
  • Vét cạn (Breadth-First Search): Trong thuật toán vét cạn, queue được sử dụng để duyệt qua các trạng thái hoặc khả năng theo cấp độ (level).
  • Queue cũng có thể được sử dụng trong các thuật toán khác như tìm kiếm theo chiều sâu (Depth-First Search), thuật toán Dijkstra và nhiều thuật toán tìm kiếm và duyệt đồ thị khác.
  • Ngoài ra Queue còn được sử dụng để khử đệ quy trong hầu hết các bài toán

6.3.2. Trong thực tế:​

  • Trong hệ thống tin nhắn: Để lưu trữ và sắp xếp các tin nhắn ngăn nắp.
  • Trong hệ thống hàng hóa vận chuyển: Giúp kiểm soát lưu lượng và đảm bảo đúng thứ tự vận chuyển.
  • Trong hệ thống giao thông: Quản lí phương tiện để đảm bảo lưu thông thuận lợi.
    …

6.4. Thao tác trên Queue​

6.4.1. Thao tác trên mảng​

Khởi tạo queue rỗng

void createQueue(QUEUE& q) {
	q.front = -1;
	q.rear = -1;
}

Kiểm tra queue rỗng

bool isEmpty(QUEUE q) {
	if (q.front == -1) {
		return 1;
	}
	return 0;
}

(*) Queue rỗng hàm trả về true (1) ngược lại trả về false (0)

Kiểm tra queue đầy

bool isFull(QUEUE q) {
	if (q.rear - q.front + 1 == MAX) {
		return 1;
	}
	return 0;
}

(*) Queue đầy hàm trả về true (1) ngược lại trả về false (0)

Thêm một phần tử vào queue

void enQueue(QUEUE& q, char x) {
	int f, r;
	if (isFull(q) == 1) {
		cout << "Queue da day, khong the them phan tu!\n";
	}
	else {
		if (q.front == -1) {
			q.front = 0;
			q.rear = -1;
		}
		if (q.rear == MAX - 1) { //Queue đầy ảo
			f = q.front;
			r = q.rear;
			for (int i = f; i <= r; i++) {
				q.a[i - f] = q.a[i];
			}
			q.front = 0;
			q.rear = r - f;
		}
		q.rear++;
		q.a[q.rear] = x;
	}
}

Thực hiện EnQueue

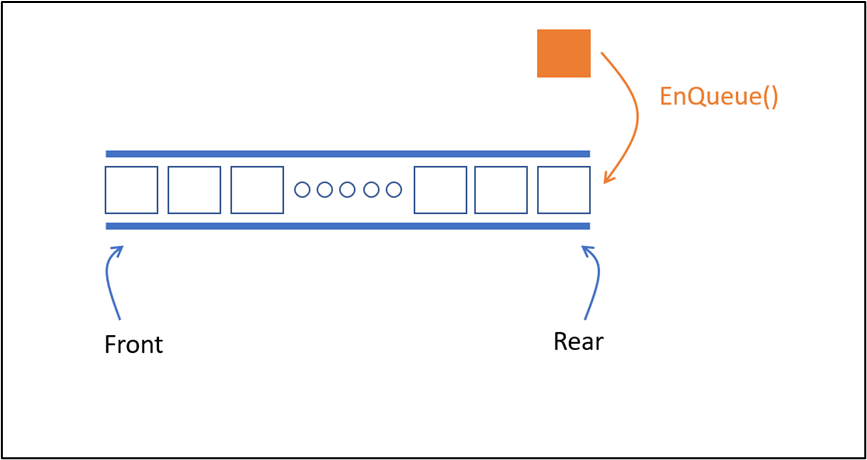
Queue sau khi EnQueue


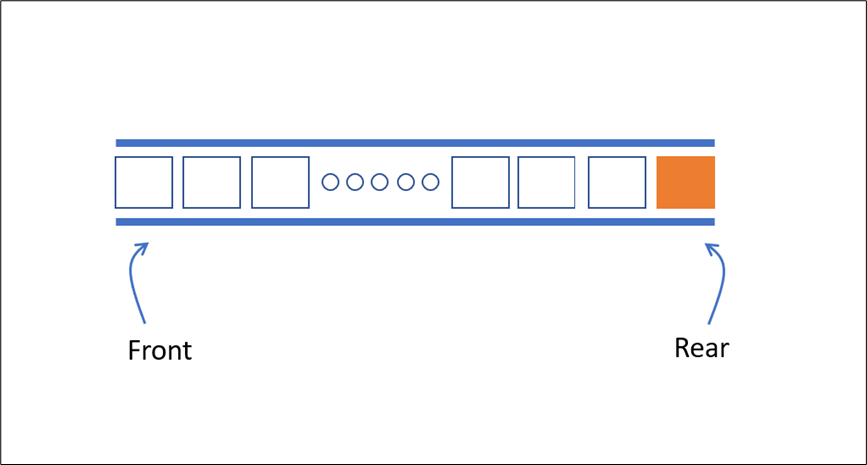
(*) Sau khi thực hiện EnQueue() độ dài queue tăng thêm 1

Lấy một phần tử ra khỏi queue

bool DeQueue(QUEUE& q, int& x)
{
	if (isEmpty(q) == 0)
	{
		x = q.a[q.Front];
		q.Front++;
		//Trường hợp queue chỉ có 1 phần tử => khi lấy ra queue rỗng
		if (q.Front > q.Rear)
		{
			q.Front = -1;
			q.Rear = -1;
		}
		return 1;
	}
	cout << "Queue rong!";
	return 0;
}

Khi thực hiện DeQueue

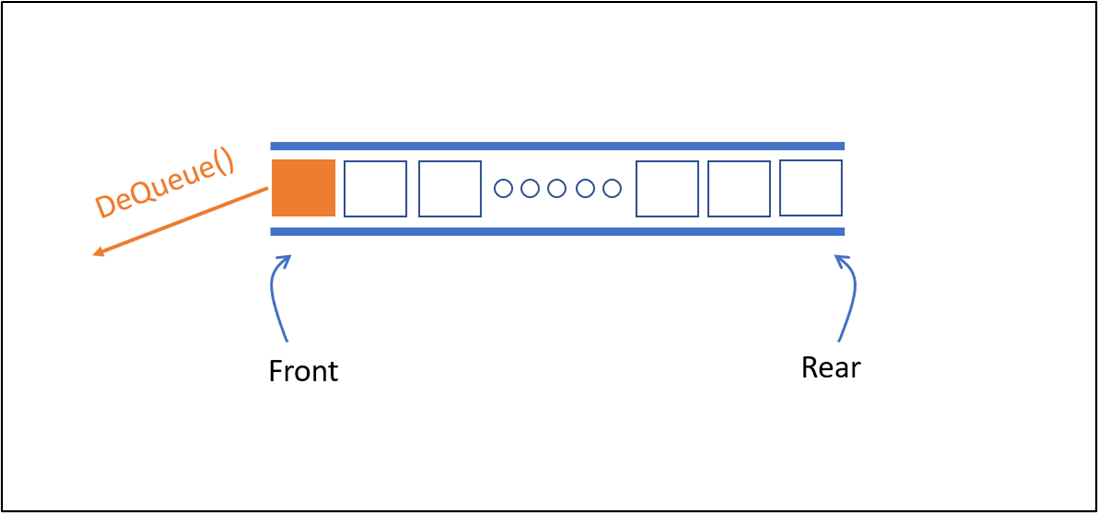
Sau khi thực hiện DeQueue


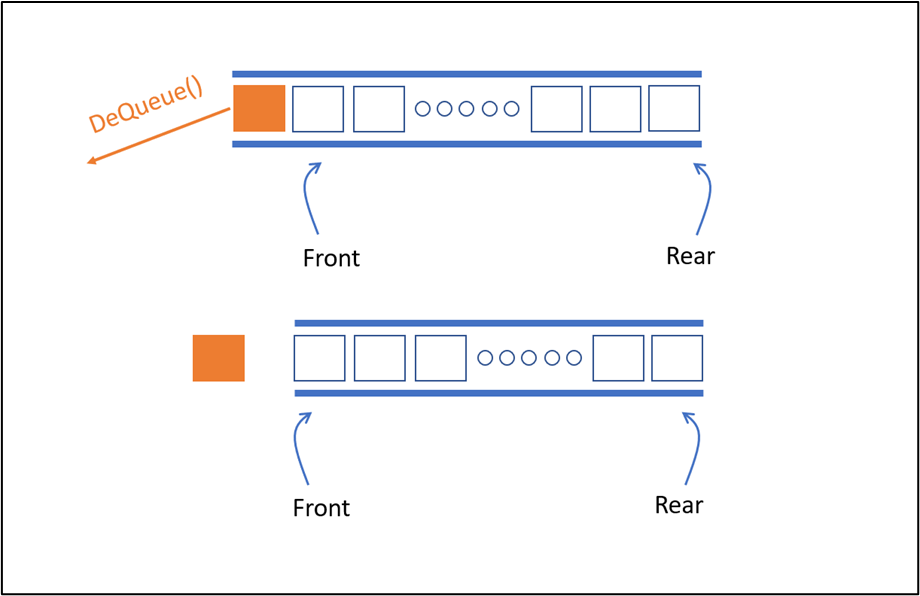
(*) Sau khi thực hiện DeQueue độ dài queue giảm đi 1

6.4.2. Thao tác trên danh sách liên kết đơn​

Khởi tạo queue rỗng

void createQueue(QUEUE& q) {
	q.front = NULL;
	q.rear = NULL;
}

Kiểm tra queue rỗng

bool isEmpty(QUEUE& Q) {
	if (Q.front == NULL) { //Queue rỗng
		return 1;
	}
	return 0;
}

Thêm một phần tử vào queue

void enQueue(QUEUE& Q, Node* p) {
	if (Q.front == NULL) {
		Q.front = Q.rear = p;
	}
	else {
		Q.rear->next = p;
		Q.rear = p;
	}
}

Trước khi EnQueue

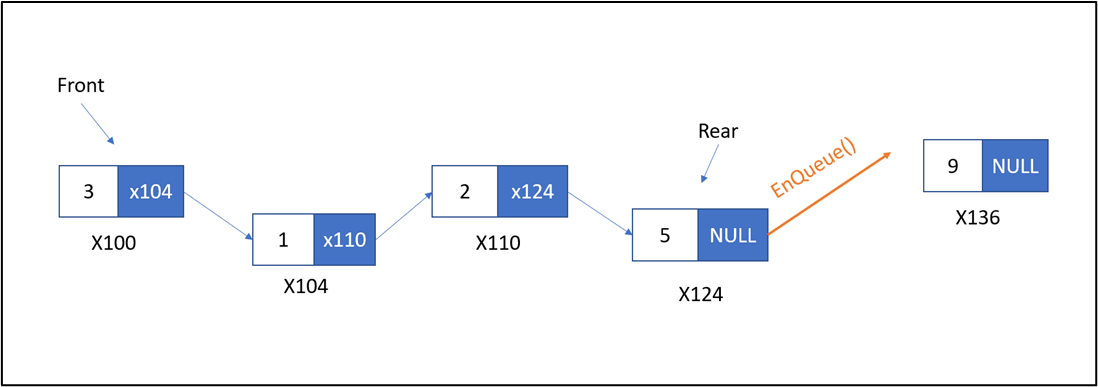
Sau khi EnQueue

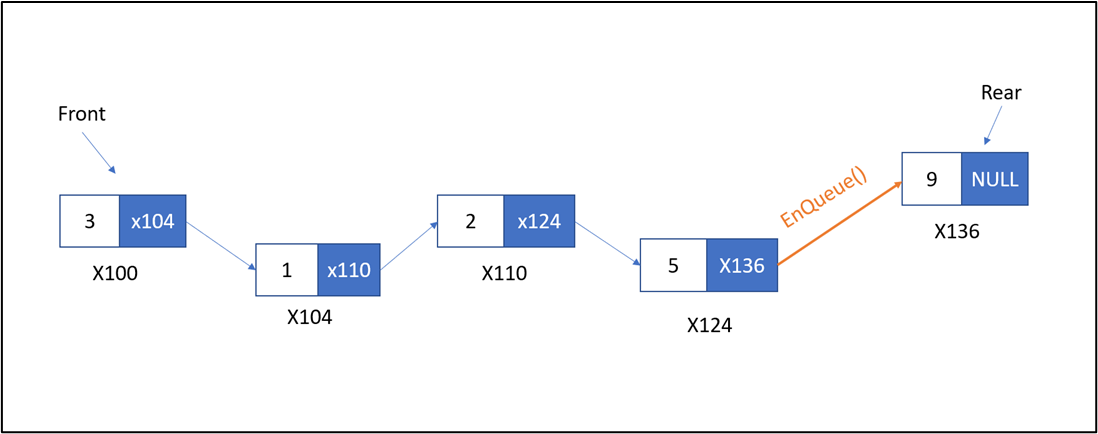
  • Node tiếp theo (pNext) của node Rear (X124) sẽ giữ địa chỉ node được thêm vào (X136)
  • Node Rear hiện tại chuyển thành node vừa được thêm vào (X136)
  • Hàm EnQueue trong danh sách liên kết đơn tương tự như hàm AddTail

Lấy một phần tử ra khỏi queue

int deQueue(QUEUE& Q, int& x) {
	Node* p;
	if (isEmpty(Q) == 0) {
		p = Q.front;
		x = p->data;
		Q.front = Q.front->next;
		//Nếu ban đầu queue có 1 phần tử, sau khi DeQueue thì queue rỗng
		if (Q.front == NULL) {
			Q.rear = NULL;
		}
		return 1;
	}
	return 0;
}

Trước khi DeQueue

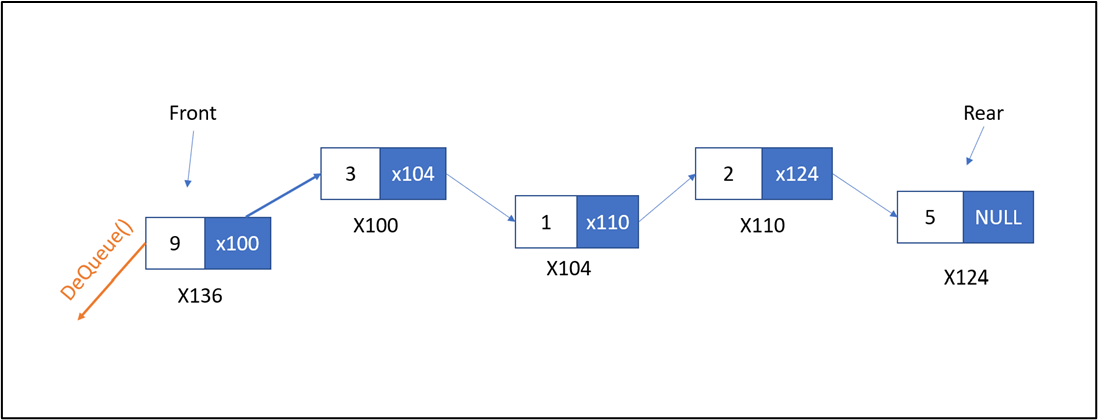
Sau khi DeQueue

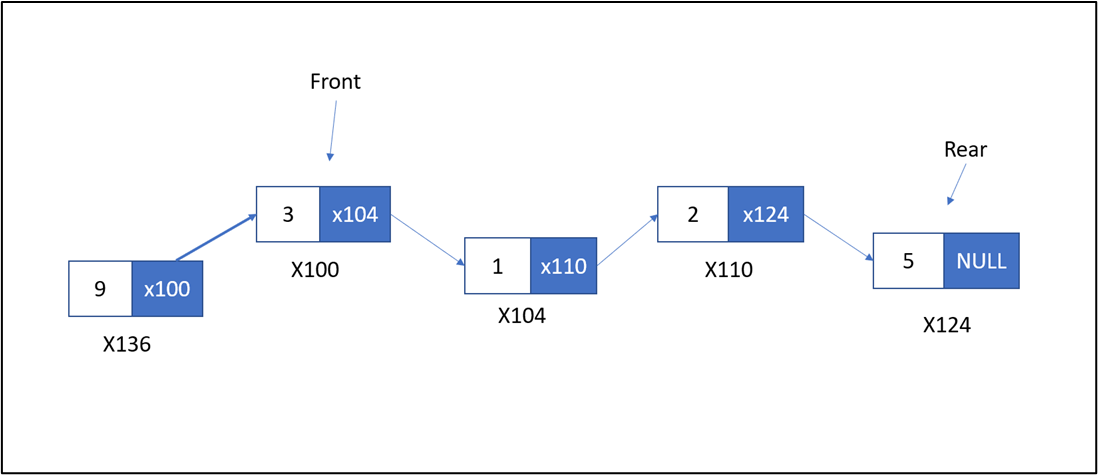(!) Nhận xét: Để hoàn thiện chương trình, ngoài các hàm thao tác ra chúng ta cần tạo thêm một số hàm như là CreateNode (Tạo node trong danh sách liên kết đơn), hàm Input (Nhập vào queue), hàm Output (Xuất các phần tử trong queue),…

6.5. Bài toán thường gặp​

6.5.1. Chuỗi palindromes​

  • Khái niệm: Một chuỗi palindromes là một chuỗi có thể được đọc xuôi hay ngược mà vẫn cho kết quả giống nhau.
  • Ví dụ: "level" và "radar".

Giải thuật sử dụng queue:

  • Ta có thể sử dụng một queue để kiểm tra palindrome bằng cách: đẩy nửa cuối chuỗi vào queue, sau đó so sánh các ký tự còn lại với các ký tự được lấy từ queue. Nếu tất cả các ký tự khớp, chuỗi là palindrome.
  • Độ phức tạp: O(n/2), n: là độ dài của chuỗi.

Cài đặt hàm tham khảo:

bool isPalindromes(string str) {
	QUEUE q;
	createQueue(q);
	int n = str.size();
	// Đưa nửa sau hàng đợi vào chuỗi
	for (int i = n - 1; i > n/2; i--) {
		enQueue(q, str[i]);
		str.pop_back();
	}
	// So sánh với các phần tử còn lại
	int i = 0;
	char x;
	while (!isEmpty(q)) {
		deQueue(q, x);
		if (x != str[i]) {
			return false;
		}
		i++;
	}
	return true;  
}

6.5.2. Giải thuật dermerging:​

  • Được sử dụng để phân tách một danh sách (hay mảng) gồm các phần tử có thuộc tính nhất định thành hai danh sách riêng biệt, mỗi danh sách chứa các phần tử có thuộc tính khác nhau.
  • Thông thường, thuộc tính được sử dụng để phân chia là thuộc tính boolean, ví dụ: giới tính (nam, nữ), trạng thái (đã kích hoạt, chưa kích hoạt),…
  • Độ phức tạp: O(n/2), n: là độ dài của chuỗi.

6.5.3. Chuyển từ biểu thức trung tố sang ký pháp Ba Lan​

6.6. Bài tập​

Bài 1 Tạo số nhị phân từ 1 đến N bằng cách sử dụng Hàng đợi

#include <bits/stdc++.h>
using namespace std;  

// Hàm chuyển số nhị phân (dạng số nguyên) sang thập phân
int dec(int n) 
{
    int ans = 0;  // Biến lưu kết quả thập phân
    string s = to_string(n);  // Chuyển số n thành chuỗi để dễ duyệt từng chữ số
    // Duyệt từng chữ số từ phải sang trái (bit thấp đến bit cao)
    for (int i = s.size() - 1; i >= 0; --i) 
    {
        int index = (s.size() - 1 - i);  // index = số mũ của 2 tương ứng với vị trí bit hiện tại
        // Cộng vào ans: giá trị bit * 2^index
        ans += (s[i] - '0') * (1 << index);  // 1 << index chính là 2^index
    }
    return ans;  // Trả về giá trị thập phân
}
int main() 
{
    int n; 
    cin >> n;   // Nhập n từ bàn phím
    queue<int> q;  // Khởi tạo queue để sinh dãy số nhị phân
    // Xử lý trường hợp đặc biệt: n = 0
    if (n == 0) 
    {
        cout << 0;  // In ra 0
        return; 
    } 
    // Nếu n != 0
    // Đầu tiên, đẩy số 1 vào queue (bắt đầu sinh từ 1)
    q.push(1); 
    // In số 0 trước vì thuật toán sinh bên dưới sẽ chỉ sinh được các số ≥ 1
    cout << 0 << endl; 
    // Vòng lặp BFS để sinh tất cả các số nhị phân hợp lệ ≤ n
    while (q.size()) 
    {
        int t = q.front(); q.pop();  // Lấy phần tử đầu queue ra
        // In ra số t (hiện đang ở dạng "nhị phân" biểu diễn bằng số nguyên)
        cout <<  t << endl; 
        // Sinh các số mới bằng cách gắn '0' hoặc '1' vào cuối số hiện tại
        // Nếu số t * 10 (tức là thêm '0') vẫn có giá trị thập phân ≤ n thì push vào queue
        if (dec(t * 10) <= n) 
            q.push(t * 10); 
        // Nếu số t * 10 + 1 (tức là thêm '1') vẫn có giá trị thập phân ≤ n thì push vào queue
        if (dec(t * 10 + 1) <= n) 
            q.push(t * 10 + 1); 
    }
}

Bài 2 Cho một chuỗi s chỉ chứa các ký tự '(', ')', ', ', '[' và ']', hãy xác định xem chuỗi đầu vào có hợp lệ hay không.

Gợi ý:

  1. Một chuỗi đầu vào hợp lệ nếu:
  2. Dấu ngoặc mở phải được đóng bằng cùng một loại dấu ngoặc.
  3. Dấu ngoặc mở phải được đóng theo đúng thứ tự.
  4. Mỗi dấu ngoặc đóng có một dấu ngoặc mở tương ứng cùng loại.
#include <bits/stdc++.h>
using namespace std; 

// Hàm kiểm tra xem chuỗi s có dấu ngoặc hợp lệ hay không
bool isValid(string s) 
{
    stack<char> st;  // Stack để lưu dấu ngoặc mở
    // Duyệt từng ký tự trong chuỗi s
    for (int i = 0; i < s.size(); ++i) 
    {
        // Nếu là dấu ngoặc mở '[' hoặc '(', đẩy vào stack
        if (s[i] == '[' || s[i] == '(') 
            st.push(s[i]); 
        // Nếu là dấu đóng ']'
        if (s[i] == ']') 
        {
            // Nếu stack rỗng hoặc top không phải là dấu mở tương ứng '[', trả về false
            if (st.empty() || st.top() != '[') 
                return 0; 
            else 
                st.pop();  // Nếu hợp lệ, bỏ dấu mở ra khỏi stack
        }
        // Nếu là dấu đóng ')'
        if (s[i] == ')') 
        {
            // Nếu stack rỗng hoặc top không phải là dấu mở tương ứng '(', trả về false
            if (st.empty() || st.top() != '(') 
                return 0; 
            else 
                st.pop();  // Nếu hợp lệ, bỏ dấu mở ra khỏi stack
        }
    }
    // Sau khi duyệt hết chuỗi:
    // Nếu stack còn phần tử → còn dấu mở chưa đóng → không hợp lệ → return false
    if (st.size()) 
        return 0; 
    // Nếu stack rỗng → tất cả dấu mở đều đã được đóng đúng → hợp lệ → return true
    return 1; 
}
int main() 
{
    string s; 
    cin >> s;   
    bool ans = isValid(s);  // Kiểm tra xem s có hợp lệ không
    // In ra kết quả
    if (ans) 
        cout << "YES\n"; 
    else 
        cout << "NO\n"; 
}

Bài 3 Viết chương trình chuyển biểu thức trung tố sang biểu thức ký pháp Ba Lan sử dụng queue.

#include <bits/stdc++.h>
using namespace std;

// Khai báo map để lưu độ ưu tiên của các toán tử
map<char, int> mp; 
// Hàm cài đặt độ ưu tiên cho từng loại toán tử
void setUp() 
{
    // Độ ưu tiên mặc định của lính canh '0' là 0 (thấp nhất)
    mp['0'] = 0; 

    // Độ ưu tiên của + và - là 1
    mp['+'] = mp['-'] = 1;

    // Độ ưu tiên của * và / là 2
    mp['*'] = mp['/'] = 2; 
}
// Hàm chuyển đổi biểu thức trung tố (infix) sang hậu tố (postfix)
// Trả về queue chứa biểu thức hậu tố
queue<char> infixToPostFix(string s) 
{
    stack<char> ope;    // Stack lưu toán tử tạm thời
    queue<char> ans;    // Queue lưu kết quả hậu tố
    // Đặt lính canh '0' vào stack để tránh stack bị rỗng khi kiểm tra
    ope.push('0'); 
    // Duyệt qua từng ký tự trong chuỗi đầu vào
    for (int i = 0; i < s.size(); ++i) 
    {
        // Nếu là số (operand), thì đưa thẳng vào queue kết quả
        if (s[i] >= '0' && s[i] <= '9') 
            ans.push(s[i]);  

        // Nếu là dấu mở ngoặc '(', đẩy vào stack
        else if (s[i] == '(') 
            ope.push(s[i]); 

        // Nếu là dấu đóng ngoặc ')'
        else if (s[i] == ')') 
        {
            // Đưa toàn bộ toán tử từ stack ra queue cho đến khi gặp '('
            while (ope.top() != '(') 
            {
                char ch = ope.top(); ope.pop(); 
                ans.push(ch); 
            } 
            // Bỏ dấu '(' ra khỏi stack
            ope.pop(); 
        } 
        else 
        {
            // Nếu là toán tử (+ - * /), xử lý theo độ ưu tiên:
            // Đưa toán tử có độ ưu tiên >= toán tử hiện tại từ stack ra queue
            while (mp[ope.top()] >= mp[s[i]]) 
            {
                char ch = ope.top(); ope.pop(); 
                ans.push(ch); 
            } 
            // Đẩy toán tử hiện tại vào stack
            ope.push(s[i]); 
        }
    }
    // Sau khi duyệt hết chuỗi, đưa toàn bộ toán tử còn lại trong stack ra queue
    while (ope.size()) 
    {
        char ch = ope.top(); ope.pop(); 
        ans.push(ch); 
    } 

    // Trả về queue chứa kết quả hậu tố
    return ans; 
} 
int main() 
{
    string s; 
    cin >> s;         
    setUp();           // Cài đặt độ ưu tiên toán tử
    queue<char> q = infixToPostFix(s);  // Chuyển sang hậu tố (postfix)
    vector<char> ans;  // Vector lưu kết quả để dễ xuất ra màn hình
    // Chuyển từng phần tử từ queue sang vector để in ra
    // Chú ý: ở đây vòng lặp có số vòng = độ dài của chuỗi đầu vào
    for (int i = 0; i < s.size(); ++i) 
    {
        ans.push_back(q.front()); 
        q.pop(); 
    } 
    // In ra kết quả hậu tố cách nhau bởi dấu cách
    for (auto x : ans) 
        cout << x << ' '; 
}