Chương 7: Cây (Tree)

7.1. Cấu trúc cây

7.1.1. Định nghĩa

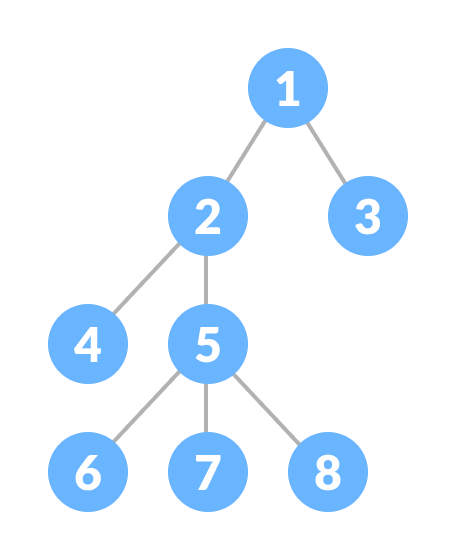
Cây là một cấu trúc dữ liệu phi tuyến tính (non-linear data structure). Trong đó, tập hợp các phần tử được gọi là các nút (node) được kết nối với nhau thông qua các cạnh, sao cho chỉ tồn tại đúng một đường đi giữa 2 nút bất kì.

Note: Dữ liệu trong cây không được lưu trữ theo cách tuần tự, tuyến tính mà được sắp xếp phân cấp. Vì vậy, cây được gọi là CTDL phi tuyến tính

7.1.2. Tính chất

1. Cây là một đồ thị vô hướng, không có chu trình

• 1. Mỗi cặp đỉnh trong cây luôn có đúng một đường đi duy nhất giữa chúng.
• 2. Để quản lí một cây, ta sẽ quản lí một nút gọi là nút gốc của cây (root node). Từ nút gốc có thể duyệt đến mọi nút khác trong cây
• 3. Một cây có n đỉnh thì có đúng n-1 cạnh: Đây là tính chất đặc trưng giúp phân biệt cây với các đồ thị khác

7.2. Một số khái niệm liên quan

7.2.1 Các loại node

• Node cha (Parent Node): bất kỳ node nào ngoại trừ node gốc mà có một cạnh hướng lên một node khác thì được gọi là node cha.

  -Ví dụ: {B} là node cha của {D, E , F}.

• Node con (Child Node): node ở dưới một node đã cho được kết nối bởi cạnh dưới của nó được gọi là node con của node đó.

  -Ví dụ: {G, H} là các node con của {C}.

• Node gốc (Root node): node trên cùng của cây hoặc node không có node cha nào được gọi là root node.

  Note: Có một số cây có thể không có nút gốc ()

  -Ví dụ: {A} là root node của cây.

• Node lá hoặc Node ngoài (Leaf/External Node): Các node không có bất kỳ node con nào được gọi là node lá.

  -Ví dụ: {D, I , J , F , K , H} là các node lá của cây.

7.2.2. Quan hệ giữa các node

• Tổ tiên (Ancestor): Bất kỳ node tiền nhiệm nào trên đường dẫn từ gốc đến node đó được gọi là tổ tiên của node đó.

  -Ví dụ:{A, B} là các node tổ tiên của {D}.

• Con cháu (Descendant): Một node x là con cháu của một node y nếu và chỉ nếu y là tổ tiên của x.

  -Ví dụ:{D} là node cháu của {A}.

• Anh em (Siblings): Các node con của cùng một node cha được gọi là anh em.

  Ví dụ: {D, E} là hai node anh em.

• Cây con (Subtree): Bất kỳ node nào của cây cùng với các node con của nó tạo thành một cây con.

7.2.3. Đường đi, mức, chiều cao của cây.

• Độ dài đường đi: Là số nhánh (cạnh) cần đi qua kể từ node gốc (root) đến node x (!!không tính trọng số)

Note: Đôi khi nó còn được định nghĩa là số đỉnh tính từ node gốc (root) đến node x. Tùy vào góc nhìn của mọi người thôi.

Xét Ví dụ cho cây ở 7.2.

• Ví dụ: độ dài từ A đến D là 2.

• Bậc của một node (Degree): Số lương node con trực tiếp của một node.

  • Ví dụ: Bậc của A là 2, của B là 3.

• Độ sâu của một node (Depth/Level): Số cạnh từ node gốc đến node đó. Cho biết node đó nằm sâu bao nhiêu tầng. Level/Degree của root bằng 0.

  • Ví dụ: Độ sâu của H là 2, của K là 3.

• Chiều cao của cây (Height): là mức lớn nhất của các node lá.

  • Ví dụ: Cây trên có chiều cao là 3.

7.3. Ứng dụng

Ta có thể liệt kê một số ứng dụng của cây trong lĩnh vực máy tính: Lưu trữ thông tin tự nhiên tạo thành một hệ thống phân cấp.

• Hệ thống tệp trên máy tính: Linux sử dụng Red-Black Tree để quản lí inode và tìm kiếm tập tin nhanh, Btree được sử dụng trong các database: MySQL, PostgreSQL...

• Mô hình DOM của trang HTML cũng là cây, trong đó chúng ta có thẻ HTML làm gốc, phần đầu và phần thân là các thẻ con và các thẻ này, sau đó có các thẻ con riêng của chúng. Vui lòng tham khảo Ứng dụng, Ưu điểm và Nhược điểm của Cây để biết chi tiết.

Bài viết tham khảo

• https://www-geeksforgeeks-org.translate.goog/introduction-to-tree-data-structure/?_x_tr_sl=en&_x_tr_tl=vi&_x_tr_hl=vi&_x_tr_pto=tc

• https://codelearn.io/learning/cau-truc-du-lieu-va-giai-thuat?activityType=12&activityId=1307

---

7.4. Cây nhị phân

7.4.1. Định nghĩa

Định nghĩa

Cây nhị phân là một loại cấu trúc dữ liệu cây trong đó mỗi node có thể có tối đa hai node con, một node con trái và một node con phải.

Note: Cây rỗng cũng là một cây nhị phân

7.4.2. Tính chất

• Số lượng node tối đa ở mức (tầng) $k$: $M = 2^{k - 1}$

• Tổng số node tối đa trong cây nhị phân với chiều cao $h$: $N = 2^h - 1$

7.5 Cây nhị phân tìm kiếm (BST)

7.5.1. Định nghĩa

Trong bài viết này, chúng ta sẽ chủ yếu tìm hiểu về một cây nhị phân đặc biệt gọi là Cây nhị phân tìm kiếm (Binary Search Tree - BST)

Trong BST, tất cả các phần tử của cây con bên trái của node k phải nhỏ hơn dữ liệu của node k và tất cả các phần tử của cây con bên phải của node k phải lớn hơn dữ liệu của node k. Đây được gọi là thuộc tính cây tìm kiếm nhị phân. Lưu ý rằng, thuộc tính này phải được thỏa mãn tại mọi node trong cây.

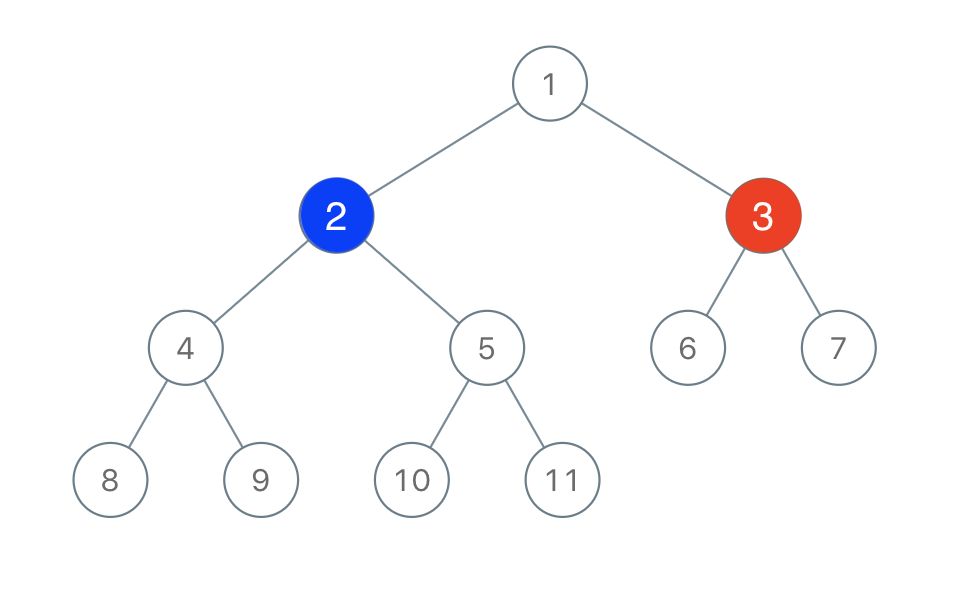
Nhờ có thuộc tính đặc biệt này mà BST mang lại cho chúng ta một số lợi ích:

• Các thuật toán như duyệt, tìm kiếm, chèn và xóa trở nên dễ hiểu hơn, dễ triển khai hơn và chạy nhanh hơn.
• Việc tổ chức dữ liệu trên cây nhị phân tìm kiếm sẽ tiết kiệm hiệu quả hơn các cấu trúc tuyến tính như mảng

Độ phức tạp một số thao tác trong BST

Thao tác	Trường hợp tốt nhất	Trung bình	Trường hợp xấu nhất
Tìm kiếm	O(1)	O(log n)	O(n)
Chèn	O(1)	O(log n)	O(n)
Xóa	O(log n)	O(log n)	O(n)

Note về cây nhị phân tìm kiếm

1. Việc tìm kiếm dữ liệu trên cây nhị phân diễn ra nhanh chóng nhờ vào khả năng chọn cây con bên trái hay cây con bên phải để xét với giá trị cần tìm.
2. Các thác cơ bản có thể thực hiện trên BST là chèn, xóa và tìm kiếm phần tử. Trong quá trình thực hiện các thao tác này, có thể làm ảnh hưởng đến chiều cao của cây. Do đó, sẽ tồn tại các biến thể về độ phức tạp thời gian của trường hợp tốt nhất, xấu nhất và trung bình
3. Thời gian thực hiện các thao tác của BST tỉ lệ thuận với chiều cao của cây. Như đã giải thích ở trên, các thao tác đó có thể ảnh hưởng tới chiều cao cây. Trong trường hợp xấu nhất, BST có thể suy biến trở thành Linked List, lúc này các thao tác sẽ khi thực hiện sẽ có độ phức tạp O(N).

7.5.2. Xây dựng cấu trúc cây nhị phân

Cấu trúc 1 node

Cấu trúc một node của cây nhị phân gồm:

• Thành phần thông tin: chứa dữ liệu của node (int, float...)
• Thành phần liên kết: Con trỏ lần lượt lưu địa chỉ node con bên trái (left) và node con bên phải (right)

struct node { 
    int data; 
    node* left; 
    node* right; 
}; 
#define node* NODE; 

Tạo hàm makeNode(x)

Hàm này quan trọng và sử dụng trong việc xây dựng BST. Hàm sẽ xin cấp phát 1 ô nhớ để lưu một giá trị x và trả về địa chỉ ô nhớ đó.

node *makeNode(int x) 
{
    node *p = new node; 
    if (p == NULL) return NULL; //Cap phat that bai, tra ve dia chi NULL 
    p->data = x; 
    return p; 
}

Để quản lí một cây nhị phân tìm kiếm, ta chỉ cần quản lí node gốc: node* root = NULL;

7.5.3.1. Các thao tác trên cây nhị phân

a. Tạo cây rỗng

void init(NODE &root) { 
    root->left = root->right = NULL;  
}; 

b. Thêm node

Ta bắt đầu từ node gốc. Nếu giá trị root->data > x thì tiến hành tìm kiếm ở cây con bên trái, ngược lại nếu root->data < x thì tiến hành tìm kiếm ở cây con bên phải. Nếu di chuyển đến 1 vị trí NULL thì tiến hành chèn node mới tại vị trí đó. Nếu tìm được 1 node có data = x thì dừng việc thêm node vì đã tồn tại.

bool insertNode(NODE &root, int x) 
{
  if (!root) {
    root = makeNode(x): 
    return 1; //Them thanh cong 
  }
  if (root->data > x) return insertNode(root->left , x); 
  else if (root->data < x) return insertNode(root->right , x); 
  return 0; //Trong truong hop node mang gia tri x da ton tai thi khong them node 
}

• Độ phức tạp: $O(\log N)$ trong trường hợp tốt nhất, $O(N)$ trong trường hợp xấu nhất

c. Tìm kiếm

Yêu cầu: Viết hàm tìm kiếm giá trị x trong cây Nhị phân tìm kiếm

Ta bắt đầu duyệt cây từ node gốc. Nếu giá trị x lớn hơn giá trị node hiện tại thì tiến hành tìm kiếm ở cây con bên phải (root->right). Nếu giá trị x nhỏ hơn giá trị node hiện tại thì tiến hành tìm kiếm ở cây con bên trái (root->left)

bool searchNode(NODE root, int x) 
{
  if (!root) return false; 
  if (root->data == x) return true; 
  if (x < root->data) return searchNode(root->left , x); 
  else if (x > root->data) return searchNode(root->right , x); 
  return false; 
}

Mở rộng: Cài đặt hàm lowerbound và upperbound của một mảng

Xét một mảng a gồm các số nguyên

lowerbound(x): Giá trị lớn nhất và nhỏ hơn x trong mảng a (lowerbound(x) < x)

upperbound(x): Giá trị nhỏ nhất và lớn hơn x trong mảng a (upperbound(x) < x)

Node: Định nghĩa này cũng có thể phụ thuộc vào cách hiểu của một số người. Có một số người qui định lowerbound <= x

Bài toán này có thể giải quyết nhanh chóng bằng set của thư viện STL hoặc giải thuật Binary search. Ở đây, tôi sẽ trình bày cách xử lí bằng cây BST (vì dô thi có thể bị cấm xài thư viện)

Trước tiên, hãy biểu diễn mảng a thành cây BST bằng thao tác insertNode đã trình bày ở trên

Biến đổi thao tác searchNode một chút sẽ có được hàm lowerbound và upperbound.

Cài đặt hàm lowerbound(x)

bool lowerbound(NODE root, int x) {
    int ans = -1; 
    while (root) {
        if (root->data < x) {
            ans = root->data;
            root = root->right;
        } else root = root->left;
    }
    return ans; 
}

Cài đặt hàm upperbound(x)

int upperbound(NODE root, int x) {
    int ans = -1; 
    while (root) {
        if (root->data > x) {
            ans = root->data;
            root = root->left;
        } else root = root->right;
    }
    return ans;
}

`

d. Duyệt cây

Có nhiều kỹ thuật duyệt cây, chúng quyết định thứ tự các node của cây sẽ được truy cập và được định nghĩa như dưới đây:

1. Duyệt theo chiều rộng: BFS

2. Duyệt theo chiều sâu: DFS. DFS được chia thành 3 nhánh nhỏ hơn

   • Inorder Traversal: LNR, RNL

   • Preorder Traversal: NLR, NRL

   • Postorder Traversal: LRN, RLN

Các phép duyệt cây cho độ phức tạp $O(N)$ chính là số node của cây

Left - Node - Right (LNR)

Trong phép duyệt này, cây con bên trái sẽ được truy cập đầu tiên, sau đó là node gốc, và cuối cùng là cây con bên phải. Tiếp tục áp dụng thứ tự truy cập này cho các cây con, ta sẽ truy cập được toàn bộ các node của cây.

void LNR(NODE root)
{ 
    if(root) { 
        LNR(root->left); 
        cout << root->data << ' '; 
        LNR(root->right); 
    } 
} 

Trong BST, các giá trị in ra sẽ tăng dần khi duyệt theo thứ tự này

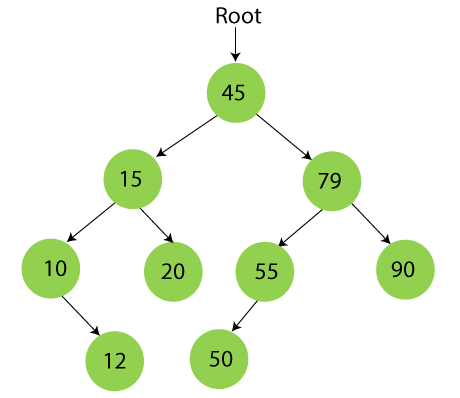
🧠 Bước duyệt chi tiết:

Bước	Hành động	Ghi lại
1	Từ gốc 8, đi sang trái → 3
2	Từ 3, đi sang trái → 1
3	1 không có con trái hay phải → thăm 1	1
4	Trở lại 3 → thăm 3	3
5	Đi phải của 3 → 6
6	Trái của 6 là 4 → thăm 4	4
7	Trở lại 6 → thăm 6	6
8	Phải của 6 là 7 → thăm 7	7
9	Trở lại 8 → thăm 8	8
10	Phải của 8 là 10 → thăm 10	10
11	Phải của 10 là 14
12	Trái của 14 là 13 → thăm 13	13
13	Trở lại 14 → thăm 14	14

Kết quả: 10, 12, 15, 20, 45, 50, 55, 79, 90

Node - Left - Right (NLR)

Trong phép duyệt này, node gốc sẽ được truy cập đầu tiên, sau đó sẽ tiến hành truy cập cây con bên trái và cuối cùng là cây con bên phải. Tiếp tục áp dụng thứ tự duyệt này cho các cây con, ta sẽ truy cập được toàn bộ các node của cây.

void NLR(NODE root)
{ 
    if(root) { 
        cout << root->data << ' '; 
        NLR(root->left); 
        NLR(root->right); 
    } 
} 

Kết quả: 45, 15, 10, 12, 20, 79, 55, 50, 90

Left - Right - Node (LRN)

Ở phép duyệt này, node gốc sẽ được duyệt cuối cùng, đầu tiên ta sẽ tiến hành duyệt cây con bên trái, tiếp theo là đến cây con bên phải và cuối cùng là duyệt node gốc.

void LRN(NODE root)
{ 
    if(root) { 
        LRN(root->left); 
        LRN(root->right); 
        cout << root->data << ' '; 
    } 
} 

Kết quả: 12, 10, 20, 15, 50, 55, 90, 79, 45

e. Xóa node trên cây

Việc xóa node sẽ phân ra làm 3 trường hợp con (học thuộc thôi @@)

TH1. Xóa node lá

Ta sẽ tiến hành xóa 1 node lá bất kỳ, ở đây ta sẽ chọn xóa node 20. Vì xóa node lá sẽ không ảnh hưởng đến cấu trúc cây, nên việc xóa node lá rất đơn giản, ta chỉ cần hủy node đó đi. Cây sau khi xóa node 29.

TH2. Xóa node có 1 con

Ở trường hợp này, ta sẽ móc nối node con của node cần xóa với node cha của node cần xóa.
Ở đây node cần xóa là node 58. node cha của node cần xóa là node 74, node con của node cần xóa là node 40. Ta sẽ thiết lập kết nối giữa node 74 và 40 rồi xóa đi node 58. Cây sau khi xóa:

TH3. Xóa node có 2 con

Ví dụ ở đây ta sẽ xóa node 18. Ta cần chọn node thay thế, ở đây có 2 cách chọn:

1. Chọn node thay thế là node nhỏ nhất của cây con bên phải (tức là node 26)

2. Chọn node thay thế là node lớn nhất của cây con bên trái (tức là node 17)

Trong trường hợp này, ta sẽ chọn node lớn nhất của cây con bên trái (tức là node 17) để thay thế.

Minh họa hàm tìm node thay thế

void replaceNode(NODE &root , NODE &p)
{ 
    if(root->right != NULL) { 
        replaceNode(root->right, p); 
        // Tìm nút phải nhất cây con trái 
    } 
    else { 
        cout<< "Nut thay the: " << root->data << endl; 
        p->data = root->data; 
        // Nút p là nút cần xóa (ta đã gán địa chỉ của root cho p ở hàm deleteNodeX), 
        // ta tiến hành gán lại data của root (nút thay thế) cho p (nút cần xóa) 
        // bây giờ ta chỉ cần xóa đi vùng nhớ của nút thay thế 
        p = root;  
        // Ta gán địa chỉ p bằng vị trí của nút thay thế 
        root = root->left; 
        // Nếu nút thay thế có cây con bên trái,  
        // nút trái của nút thay thế sẽ trở thành nút phải của nút cha nút thay thế  
    }
} 

Minh họa hàm xóa node có giá trị x

void deleteNodeX(NODE &root, int x)
{ 
    if(root != NULL) { 
        if(root->data < x) deleteNodeX(root->right, x); 
        else if(root->data > x) deleteNodeX(root->left, x); 
        else{ 
            node* p = root; 
            // ta gán địa chỉ của root cho p 
            // để sau khi tìm được nút thay thế cho root,  
            // ta tiến hành cập nhật data của nút thay thế cho vị trí này 
            if(root->left == NULL) root = root->right; 
            else if (root->right == NULL) root = root->left; 
            else replaceNode(root->left , p); 
            delete p; 
            //p bây giờ lưu địa chỉ của nút thay thế - không còn cần sử dụng nữa 
        } 
    } 
} 

Bài viết tham khảo

• https://www.geeksforgeeks.org/binary-search-tree-data-structure/

• https://codelearn.io/sharing/5-phut-thong-thao-binary-search-tree

• https://www.cs.usfca.edu/~galles/visualization/BST.html

---

7.6. B-Tree

7.6.1. Định nghĩa, tính chất

7.6.1.1 Tính chất của một node

Gồm: khóa và các cây con.

Số cây con = số khóa +1.

Minh hoạ về cây B-tree

✅ Tính chất

1. Tất cả các nút lá ở cùng một mức.
   $\rightarrow$ Cây B-tree có chiều cao cân bằng, đảm bảo hiệu quả tìm kiếm.

2. Tất cả các nút trung gian (trừ nút gốc):

   • Có tối đa $m$ cây con → tương ứng tối đa $m - 1$ khóa.
   • Có tối thiểu $\displaystyle\left\lceil \frac{m}{2} \right\rceil$ cây con khác rỗng → tương ứng với ít nhất $\displaystyle\left\lceil \frac{m}{2} \right\rceil -1$ khóa.

3. Nút có $k$ khóa:

   • Phải có đúng $k + 1$ cây con.
   • Các khóa phân chia giá trị trong các nhánh con tương tự cây tìm kiếm nhị phân:
   • Cây con thứ $i$ chứa các giá trị giữa khóa thứ $i - 1$ và khóa thứ $i$.

4. Nút gốc:

   • Nếu không là nút lá có ít nhất 2 cây con (tức là có ít nhất 1 khóa).
   • Có nhiều nhất $m$ cây con (tức là tối đa $m - 1$ khóa).
   • Nếu là cây chỉ có nút gốc, thì gốc có thể không có cây con (nút lá, không chứa khóa nào).

💡 Tips – Ghi nhớ về cây B-Tree

1. Mỗi nút chứa:
   • Một số lượng khóa từ $\displaystyle\left\lceil \frac{m}{2} \right\rceil -1$ đến $m-1$ (trừ nút gốc có thể ít hơn).
   • Số cây con $=$ số khóa $+ 1$.
2. Nút gốc:
   • Có thể là NULL hoặc nút lá (không có cây con).
   • Nếu không là lá: có ít nhất 2 cây con, nhiều nhất $m$ cây con.
3. Nút trung gian:
   • Có ít nhất $\displaystyle\frac{m}{2}$ cây con (nếu $m$ chẵn), $\displaystyle\frac{m+1}{2}$ cây con (nếu $m$ lẻ).
   • Có nhiều nhất $m$ cây con.
4. Nút lá:
   • Tất cả các nút lá nằm ở cùng một mức.
5. Khóa:
   • Các khóa trong nút được sắp xếp tăng dần như trong cây tìm kiếm nhị phân mở rộng

Xác định số cây con, số khóa tối đa, tối tiểu

Các bước tạo cây B-tree với bậc $m$:

1. Số cây con tối đa: $m$
2. Số cây con tối thiểu (cho nút trung gian): $\displaystyle\frac{m}{2}$ nếu $m$ chẵn, $\displaystyle\frac{m+1}{2}$ nếu $m$ lẻ
3. Số khóa tối đa: $m-1$
4. Số khóa tối thiểu: số cây con tối thiểu $–1$.

Ví dụ 1: Xác định số cây con tối đa, tối thiểu (cho nút trung gian), số khóa tối đa, số khóa tối thiểu (trừ nút gốc) của cây B-tree bậc 5.

• Số cây con tối đa: $5$
• Số cây con tối thiểu (cho nút trung gian): $3$
• Số khóa tối đa: $4$
• Số khóa tối thiểu (trừ nút gốc): $2$

7.6.2. Một số khái niệm thao tác với cây B-Tree

Thao tác tách nút (split)

Là thao tác sẽ được thực hiện khi thêm 1 khóa vào nút mà số khóa của nút sẽ vượt quá số khóa tối đa.

• Tiến hành lấy nút chính giữa đem gộp với nút cha của nút đang xét trở thành nút cha của 2 nút mới, 2 nút mới này chính là nút chứa các khóa bên trái và nút chứa các khóa bên phải của nút chính giữa.
• Nếu nút cha vừa được thêm khóa cũng vượt quá số khóa tối đa, ta sẽ tiếp tục thực hiện thao tác split (tách) cho nút đó.

Ví dụ 2 Cho cây B-Tree bậc 3 như sau:

Đầu tiên ta xác định số cây con, số khóa tối đa, tối thiểu.

• Số cây con tối đa: $3$
• Số cây con tối thiểu: $(3+1)/2 = 2$
• Số khóa tối đa: $3 - 1 = 2$
• Số khóa tối thiểu $(3-1)/2 = 1$

Hãy tiến hành thêm vào cây khóa có giá trị 29 sao cho cây vẫn là cây B-Tree bậc 3.

Nhìn vào cây B-Tree, thì ta xác định được vị trí phù hợp với số 29 chính là giữa nút 27, 30.

Tuy nhiên, khi ta thêm khóa 29 vào nút này thì số khóa sẽ vượt quá số khóa tối đa là 3.

Vậy nên ta sẽ tiến hành thao tác split node (tách). Khóa 29 sẽ gộp với nút cha của nút đang xét, nút 27, 30 sẽ tách thành 2 nút mới là con của nút chứa khóa 29.

Tuy nhiên, khi khóa 29 nằm ở nút 23, 32 thì số khóa của nút này cũng vượt quá số khóa tối đa, nên sẽ tiếp tục thực hiện thao tác split (tách). Cây B-Tree sau khi thực hiện xong thêm khóa 29.

Thao tác nhường khóa (underflow)

• Nếu nút sau khi xóa bớt khóa, có số khóa nhỏ hơn số khóa tối thiểu trong 1 nút, thì ta sẽ xét các nút kề của nút này.

• Nếu có nút kề có số khóa lớn hơn số khóa tối thiểu trong 1 nút, ta sẽ tiến hành nhường khóa của nút kề này cho nút đang thiếu khóa.

• Khóa được nhường sẽ lên thế chỗ 1 khóa của nút cha, khóa của nút cha sẽ vào vị trí của nút bị thiếu khóa.

Ví dụ 3 Cho cây B-Tree bậc 3 như sau, hãy tiến hành xóa nút 27 ra khỏi cây

Khi xóa nút lá 27 khỏi cây, ta thấy nút hiện hành có 0 khóa, ít hơn số khóa tối thiểu.

Ta tiến hành xét nút kề của nút 27 là nút 17, 20. Nút này có số khóa nhiều hơn số khóa tối thiểu, nên sẽ tiến hành thao tác underflow. Khóa 23 sẽ xuống thay thế cho khóa 27. Khóa 20 sẽ lên thay thế khóa 23.

Ta có cây B-tree sau khi xóa node 27

Thao tác hợp (catenate)

Trong trường hợp không có nút kề nào có số khóa lớn hơn số khóa tối thiểu, ta sẽ tiến hành thao tác catenate.

Thao tác catenate là thao tác gom các khóa của nút đang bị thiếu khóa, với nút cha và nút anh chị của nó (nút có chung khóa cha) trở thành 1 nút. Khi này, nút cha của nút bị thiếu khóa sẽ mất đi một nút, và các khóa và nút được gom sẽ trở thành nút con mới của nút cha này.

Ở nút cha có 1 khóa bị mất, 2 cây con bị mất, và 1 cây con mới được tạo. Vậy nút cha mất đi 1 khóa và 1 cây con. Nghĩa là số cây con vẫn đảm bảo hơn số khóa 1. Cấu trúc cây vẫn được đảm bảo.

Trong trường hợp, sau khi catenate, nút cha của nút vừa bị xóa khóa không đảm bảo số khóa tối thiểu $\Rightarrow$ Xem xét để thực hiện thao tác underflow, nếu không thực hiện được thao tác underflow thì ta sẽ thực hiện thao tác catenate cho nút này. Cứ thế đến khi nào không có nút nào bị thiếu số khóa tối thiểu, hoặc nút vừa gom trở thành nút gốc thì dừng việc catenate.

Ví dụ 4 Tiếp tục xóa khóa 20 khỏi cây trên.

Khi xóa khóa 20, là nút trung gian. Ta chọn 17 là khóa thế mạng của nó. Việc xóa khóa 20 quy về xóa khóa của nút lá vị trí nút khóa 17.

Ở vị trí nút lá vừa bị xóa khóa để làm khóa thế mạng, số khóa của nút hiện tại là 0, nhỏ hơn số khóa tối thiểu. Tuy nhiên, nút kề duy nhất của nút này là nút chứa khóa 23, chỉ có 1 khóa. Nên không thể thực hiện underflow. $\Rightarrow$ Ta thực hiện thao tác catenate.

Ta tiến hành gom tất cả khóa nút kề của nút đang thiếu khóa và nút cha thành một nút mới. Tức là ta gom 17, 23 thành 1 nút mới. Và làm con của nút cha hiện tại là nút chứa khóa 17. Nút 17 mất đi 1 khóa.

Tuy nhiên nút cha này, tức là nút chứa khóa 17 trước đó, lại không có khóa nào, và nút kề của nó là 32 cũng chỉ có 1 khóa, không nhiều hơn số khóa tối thiểu, nên không thể thực hiện thao tác underflow. Ta tiếp túc tiến hành catenate cho nút này.

Gom 29, 32 tạo thành nút mới, là nút con của nút 29 hiện tại.

Tuy nhiên nút cha lúc này không có khóa nào, tuy nhiên vì đây là nút gốc, nên chúng ta không cần thực hiện thao tác underflow hay catenate, mà chỉ cần cho nút 29, 32 trở thành nút gốc mới.

Cây sau khi hoàn tất xóa khóa 20:

7.6.3. Thao tác thêm nút

Thuật toán thêm khóa:

1. Xác định vị trí của khóa cần thêm.
2. Thêm khóa vào nút.
   • Nếu số khóa vượt quá số khóa tối đa, thực hiện thao tác split (tách).
   • Nếu khóa được đưa lên làm khóa cha, nằm ở nút có số khóa vượt quá số khóa tối đa khi thêm nút vừa tách, ta tiếp tục thực hiện thao tác split (tách) cho nút này.

Ví dụ 4: Hãy vẽ cây B-tree bậc 5, thêm vào cây các khóa theo thứ tự sau: 3, 7, 9, 23, 45, 1, 5, 14, 25, 24, 13, 11, 8, 19, 4, 31, 35, 56

Xác định số cây con, số khóa tối đa, tối thiểu:

• Số cây con tối đa: $5$
• Số cây con tối thiểu: $(5+1)/2 = 3$
• Số khóa tối đa: $5 - 1 = 4$
• Số khóa tối thiểu: $3 - 1 = 2$

Thêm các khóa 3, 7, 9, 23:

• Vì số khóa tối đa của 1 nút là 4, nên 4 khóa đầu tiên đều nằm ở nút gốc. Cây B-tree sau khi thêm 4 khóa 3, 7, 9, 23

Thêm khóa 45:

• Khi thêm khóa 45 vào nút hiện hành thì số nút sẽ vượt quá số khóa tối đa của 1 nút, vậy nên thao tác Split (tách) sẽ được thực hiện ở khóa số 9 và tạo thành cấu trúc mới như sau:

Thêm khóa 1:

• Vì số khóa hiện tại của nút chứa 3, 7 < số khóa tối đa. Nên có thể thêm khóa 1 vào nút đó.

Tương tự, thêm khóa 5, 14, 25:

Thêm khóa 24:

• Tương tự như khóa 45, số khóa ở nút 14, 23, 25, 45 đã đạt tối đa nên thao tác split sẽ được thực hiện. Lúc này 14, 23 và 25, 45 sẽ được tách thành nút mới, khóa 24 sẽ được tách lên đứng chung vị trí với nút 9 để làm nút cha của 2 nút vừa được tách.

• split

Thêm khóa 13, 11:

Thêm khóa 8:

• split

Thêm khóa 19:

• split

Thêm khóa 4, 31, 35:

Thêm khóa 56:

• Khóa 56 sau khi thêm vào nút 25, 31, 35, 45 thì tổng số khóa của nút này sẽ vượt quá số khóa tối đa trên 1 nút. Vậy nên nút chính giữa là 35 sẽ được tách lên làm cha của 2 nút được tách là 25, 31 và 45, 56.

• Khi khóa 35 được tách lên nằm trong nút 5, 9, 14, 24 thì số khóa của nút này lại vượt quá số khóa tối đa. Nên thao tác split (tách) sẽ được tiếp tục thực hiện ở nút này.

• Khóa chính giữa là 14 sẽ được tách lên làm cha của 2 nút được tách ra là 5, 19 và 24, 35

7.6.4. Thao tác xóa nút

Thuật toán xóa khóa:

Xóa khóa tại mọi nút được quy đổi về xóa khóa trong một nút lá. Vì khi xóa 1 nút trung gian, ta sẽ tìm nút thế mạng tương tự như khi ta xóa nút trung gian trong cây nhị phân tìm kiếm (Sẽ là nút trái nhất các cây con bên phải, hoặc nút phải nhất trong các cây con trái). Lúc này thì số lượng các khóa tại nút trung gian không bị thay đổi, và nút lá thì bị mất một khóa, nên ta có thể xem như việc xóa 1 khóa của nút lá.

• Đặt $\displaystyle k = \frac{m-1}{2}$ nếu $m$ lẻ, và $\displaystyle k=\frac{m}{2}-1$ nếu m chẵn (Chương trình UIT chỉ xét cây B-tree bậc lẻ).

• Nếu nút lá chứa khóa cần xóa có nhiều hơn $k$ khóa, thực hiện xóa khóa đó mà không sợ ảnh hưởng đến cấu trúc cây.

• Nếu nút lá chỉ chứa $k$ khóa, sau khi xóa chỉ còn $k-1$ khóa, ta thực hiện thao tác underflow:

  • Nếu một nút kề nút vừa mất khóa có nhiều hơn $k$ khóa, chuyển khóa đó sang cho nút vừa xóa đi 1 khóa.
  • Ngược lại, thực hiện catenate với một nút kề.
  • Lặp lại thao tác underflow như trên cho nút trung gian nếu nút trung gian có ít hơn $k$ khóa.

• Nếu chúng ta thực hiện catenate đến nút gốc và nút gốc chỉ còn lại 1 nút con, thì cho nút con làm nút gốc mới.

Ví dụ 5: Hãy xóa lần lượt các khóa: 4, 5, 7, 3, 14 khỏi cây B-tree trong Hình dưới

Đầu tiên, ta xác định $k = (5-1)/2 = 2$

Xóa khóa 4:

• Nút hiện tại chứa khóa 4 là nút lá, có 3 khóa $> k$. Nên ta chỉ cần xóa khóa 4 mà không sợ ảnh hưởng đến cấu trúc cây.
• Cây sau khi xóa khóa 4:

Xóa khóa 5:

• Vì khóa 5 nằm ở nút trung gian, nên ta tìm khóa thế mạng, có thể chọn khóa 3 (phải nhất cây trái) hoặc 7 (trái nhất cây phải). Ở đây, giả sử ta chọn 3 là khóa thế mạng.

• Sau khi đẩy khóa 3 lên thay thế, ta quy việc xóa khóa trung gian về xóa 1 khóa ở nút lá 1,3.

• Và nút lá 1, 3 sau khi đem khóa 3 lên thế mạng thì số khóa không đảm bảo số lượng khóa tối thiểu trong 1 nút của cây bậc 5. Xét nút kề của nút 1 là nút 7, 8 chỉ có 2 khóa (không nhiều hơn $k$ khóa) nên không thể thực hiện underflow.
• Vì vậy, ta phải thực hiện catenate:
  • Ta tiến hành gom các nút anh chị của nút 1 (có chung cha) và khóa cha của nó thành 1 nút mới (ta quy ước khóa 3 là khóa cha của nút 1 và nút 7, 8), và các nút được gom lại thành 1 nút sẽ làm con của nút chứa khóa cha. (Trong ví dụ đang xét, nút 1 chỉ có 1 khóa cha duy nhất là 3, và 1 nút anh chị duy nhất là 7, 8, nên chỉ có 1 cách gom duy nhất là gom 1, 3, 7, 8 thành 1 nút. Nếu gặp trường hợp có nhiều hơn 1 lựa chọn, tức nút 1 có 2 khóa cha và 2 nút anh chị, thì tùy theo yêu cầu xóa của đề bài để chọn gom bên nhánh anh chị nào (nếu không nói gì thêm thì cứ chọn 1 bên trái hoặc phải để gom). Như trong ví dụ trên, nút 1 chỉ có nhánh anh chị bên phải nên ta sẽ gom nó thành 1 nút mới). Và sau khi gom:

• Sau khi gom, nút 9 chỉ có 1 khóa, không đủ số khóa tối thiểu. Xét các nút kề của nút 9 thì không có nút nào có nhiều hơn $k$ khóa (2 khóa) nên không thể thực hiện underflow. Vậy nên ta sẽ tiến hành catenate, gom 9, 14, 24, 35 thành 1 nút. Lúc này, khóa của nút gốc đã bị gom lại thành nút mới 9, 14, 24, 35 nên số khóa của nút gốc chỉ còn là 0, nhưng vì nút gốc không còn khóa nào nên không cần phải thực hiện underflow hay catenate, mà nút con của nút gốc hiện tại sẽ trở thành nút gốc.

Xóa khóa 7, 3, 14

---

Bài viết tham khảo

• https://tek4.vn/khoa-hoc/cau-truc-du-lieu-va-thuat-toan/b-tree-va-ung-dung-cua-b-tree

• https://viblo.asia/p/gioi-thieu-ve-b-tree-index-trong-database-ByEZkQn25Q0