Chương 8: Đồ thị (Graph)

8.1. Lý thuyết Đồ thị

Người đặt nền móng cho sự phát triển của đồ thị là nhà toán học thụy sĩ Leonhard Euler (1707 - 1783). Trong bài toán Cầu Königsberg, Euler đã giới thiệu khái niệm về đồ thị và sử dụng nó để giải quyết bài toán này. Euler cũng đưa ra định lý Euler, nền tảng cho nhiều phát triển sau này trong lĩnh vực lý thuyết đồ thị. Thông tin về bài toán các bạn có thể tham khảo tại đây

Trong lĩnh vực Toán - Tin, lý thuyết đồ thị tập trung vào việc nghiên cứu về một đối tượng gọi là đồ thị. Chúng ta có thể dễ dàng bắt gặp ứng dụng của đối tượng này trong cuộc sống hằng ngày như: giao thông, Google Maps, cấu trúc mạng lưới Internet...

8.1.1. Khái niệm

Một đồ thị là một cấu trúc rời rạc gồm tập hợp các đỉnh và các cạnh nối giữa các đỉnh đó. Có thể mô tả đồ thị theo cách hình thức như sau: G = (V,E), trong đó $V$ là tập hợp các đỉnh, $E$ là tập hợp các cạnh

Minh hoạt đơn giản về đồ thị

Phân tích: Tập hợp V = {1 , 2 , 3 , 4}, E = (1,4) , (1,3) , (3,5) , (3,2) , (2,4) , (2,5)

Đồ thị vô hướng (Undirected Graph)

Đồ thị G = (V ,E) được gọi là đồ thị vô hướng nếu mọi cạnh trong E đều không định hướng, nghĩa là không có sự phân biệt về chiều giữa đỉnh đầu và đỉnh cuối

Đồ thị có hướng (Directed Graph)

Đồ thị G = (V ,E) được gọi là đồ thị có hướng nếu các cạnh trong E là có định hướng, nghĩa là tồn tại đường nối từ u -> v nhưng chưa chắc tồn tại đường nối từ v->u.

Trong đồ thị có hướng, mỗi cạnh nối được gọi là một cung. Một đồ thị vô hướng có thể xem là đồ thị có hướng với đầy đủ 2 cung u->v và v->u

Đồ thị có trọng số (Weighted graph)

Đồ thị có trọng số là một loại đồ thị trong đó mỗi cạnh được gán một giá trị số gọi là trọng số. Trọng số đó có thể đại diện cho một số thuộc tính: chi phí di chuyển trên cạnh, thời gian, khoảng cách giữa hai đỉnh trong đồ thị...

Đồ thị có trọng số cho phép mô hình hóa và phân tích các vấn đề phức tạp hơn trong thực tế, như tìm kiếm đường đi ngắn nhất dựa trên trọng số, tối ưu hóa đường đi dựa trên chi phí hoặc tìm kiếm cấu trúc mạng phù hợp dựa trên sự tương tự,…

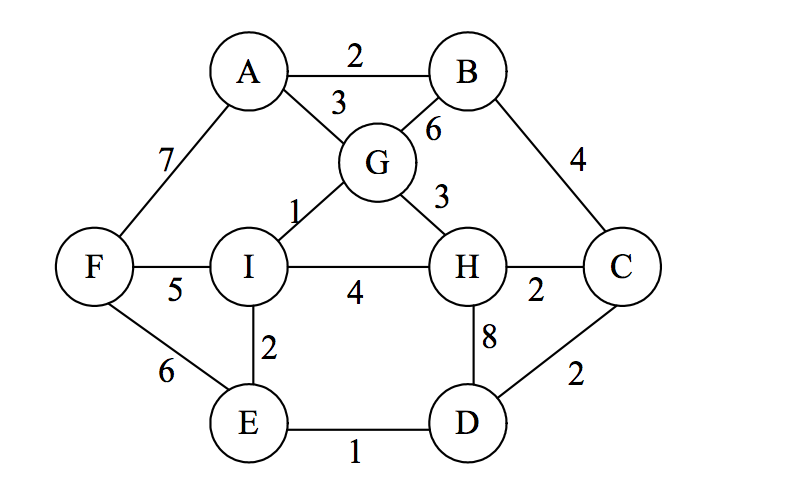
Có thể dựa vào tính chất cạnh để phân chia đồ thị thành hai dạng như sau:

Đơn đồ thị là đồ thị không có các cạnh song song (đa cạnh) giữa hai đỉnh và không có cạnh nối một đỉnh với chính nó (khuyên).

Đa đồ thị là đồ thị có các cạnh song song và tùy theo định nghĩa mà nó có khuyên hay không. Đơn đồ thị cũng là đa đồ thị

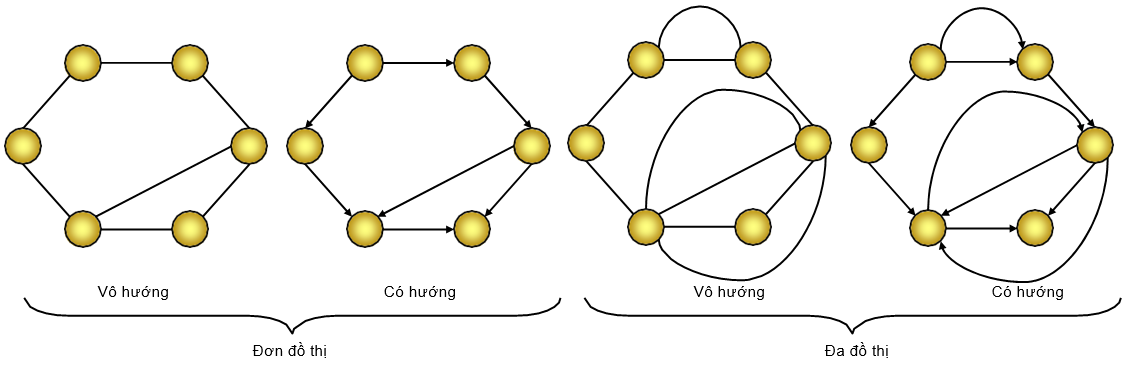
Src: https://viblo.asia/p/gioi-thieu-ve-ly-thuyet-do-thi-07LKXQ1eZV4

8.1.2. Một số đồ thị đặc biệt

Đồ thị rỗng (Null graph) là một đồ thị không chứa bất kỳ đỉnh nào. Nó không có đỉnh và không có cạnh. Trong đồ thị rỗng, không có mối quan hệ hoặc liên kết nào giữa các đỉnh, vì không có đỉnh nào tồn tại để tạo ra các mối quan hệ đó.

Đồ thị đầy đủ (Complete graph): là đồ thị trong đó mỗi cặp đỉnh bất kỳ đều được nối bằng đúng một cạnh. Ký hiệu $K_n$ với n là số đỉnh của đồ thị

Công thức tính số cạnh Đồ thị đủ: $|E| = \frac{n (n - 1)}{2}$

Đồ thị lưỡng phân (Bipartite graph) là đồ thị mà tập đỉnh của nó có thể được chia thành hai tập disjoints (không có phần tử chung) sao cho mọi cạnh chỉ nối giữa các đỉnh thuộc hai tập khác nhau, không có cạnh nối giữa hai đỉnh cùng tập.

Hình ành minh họa:

Src: https://www.sciencedirect.com/science/article/pii/S0166218X18301203

8.1.3. Chu trình, đường đi

Đường đi

Một đường đi trong G là một dãy luân phiên các đỉnh 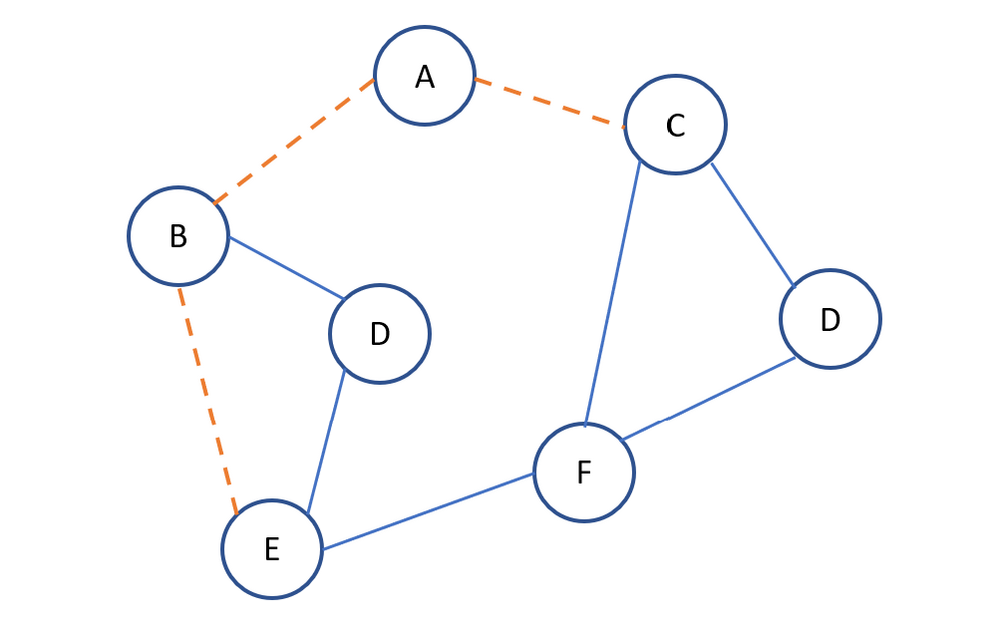$e_1, e_2, e_3,... e_m$ sao cho $(e_i-1 , e_i) ∈ E$ (*) E B A C là một đường đi

Khi đó $e_1$ được gọi là đỉnh bắt đầu và $e_m$ được gọi là đỉnh kết thúc của đường đi

Một đường đi con (subpath) là một đoạn liên tục các đỉnh dọc theo đường đi $P$

Chu trình

Một chu trình trong đồ thị là một đường đi có đỉnh đầu trùng đỉnh cuối 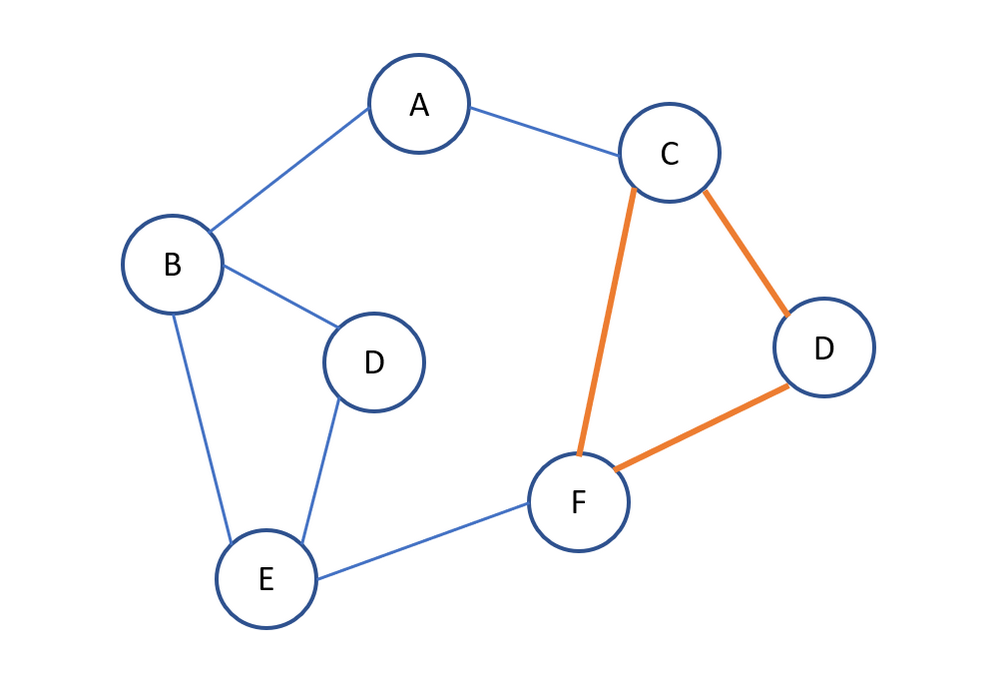(*) C, D , F là một chu trình

Tính chất đơn và sơ cấp

Tính chất "đơn" của chu trình hay đường đi: không có cạnh nào xuất hiện hai lần trong chu trình hay đường đi đó.

Chu trình đơn: là chu trình không đi qua cạnh nào quá một lần

Tính chất "sơ cấp" (hay cũng gọi là "thứ cấp"): không có đỉnh nào xuất hiện hai lần.

Chu trình sơ cấp: là chu trình không chứa một đỉnh quá một lần, trừ đỉnh đầu và đỉnh cuối

8.1.4. Bậc của đỉnh (degree)

Đồ thị vô hướng bậc của một đỉnh trong đồ thị vô hướng là số lượng cạnh kết nối với đỉnh đó. Ký hiệu bằng "deg(v)" hoặc "d(v)".

Đỉnh treo có bậc là 1
Đỉnh cô lập có bậc là 0

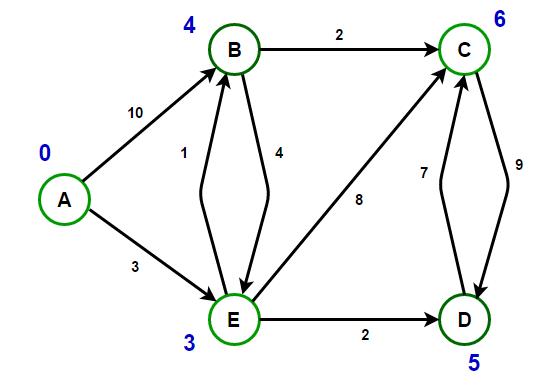
Đồ thị có hướng bậc của một đỉnh trong đồ thị có hướng là tổng số cạnh đi ra từ đỉnh đó và số cạnh đi vào đỉnh đó.

Bậc ra (outdegree): là số lượng cạnh đi ra từ một đỉnh. Ký hiệu: deg+(v)
Bậc vào (indegree): là số lượng cạnh đi vào một đỉnh. Ký hiệu deg-(v)

Ta có bậc của một đỉnh: deg(V) = deg+(V) + deg-(V)

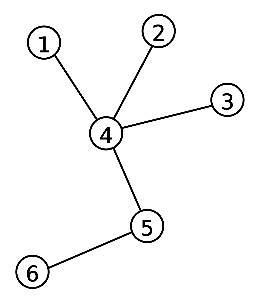
Trong đó:

1, 2, 3, 6 là đỉnh treo với bậc là 1

deg(4) = 4 và deg(5) = 2

8.1.5. Liên thông (connection)

Khái niệm liên thông cũng như thuật toán tìm thành phần liên thông sẽ phân ra khác nhau, tùy thuộc vào đó là đồ thị vô hướng hay đồ thị có hướng.

8.1.5.1. Đồ thị vô hướng

Đồ thị vô hướng G = (V, E) được gọi là liên thông nếu luôn tìm được đường đi giữa hai đỉnh bất kỳ của nó Minh hoạt về một đồ thị vô hướng liên thông

Trong trường hợp đồ thị là không liên thông, nó sẽ rã ra thành một số đồ thị con liên thông không có đỉnh chung. Những đồ thị con liên thông như vậy ta sẽ gọi là các thành phần liên thông của đồ thị. Minh hoạt về một đồ thị vô hướng liên thông

Cầu: Cầu là một cạnh mà khi bỏ cạnh đó đi sẽ làm tăng số thành phần liên thông của đồ thị

Khớp: Cầu là cạnh mà khi loại nó khỏi đồ thị thì số thành phần liên thông của đồ thị tăng lên

Khái niệm cầu và khớp có thể mở rộng sang khái niệm liên thông bên đồ thị có hướng (liên thông mạnh). Các bạn có thể tham khảo thuật toán Tarjan để tìm cầu và khớp của đồ thị tại đây để hiễu rõ hơn về sự liên quan đó

📝 Tham khảo thuật toán đếm số TPLT của đồ thị vô hướng:

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
vector<int> a[N]; 
int n,m; 
bool visited[N]; 
//Nhập thông tin và biểu diễn đồ thị dạng danh sách kề
void inp()   
{
    cin >> n >> m; 
    for (int i = 0; i < m; ++i) 
    {
        int x,y;
        cin >> x >> y; 
        a[x].push_back(y); 
        a[y].push_back(x); 
    } 
    fill(visited , visited + N, 0); 
}
void backtrack(int u) 
{
    visited[u] = 1; 
    for (auto x : a[u]) if (!visited[x]) backtrack(x); 
}
void solve()
{
    inp(); 
    int cc = 0; 
    //Duyệt qua toàn bộ đỉnh, nếu phát hiện đỉnh chưa thăm thì gọi hàm dfs(i) để thăm toàn bộ TPLT của đỉnh i và tăng số thành phần liên thông lên 1
    for (int i = 1; i <= n; ++i) if (!visited[i]) {
        ++cc; 
        backtrack(i);  
    }
    cout << cc; 
}
int main()
{
    solve(); 
    return 0; 
}

8.1.5.2. Đồ thị có hướng

Khái niệm liên thông trong đồ thị có hướng bao gồm Liên thông mạnh và Liên thông yếu

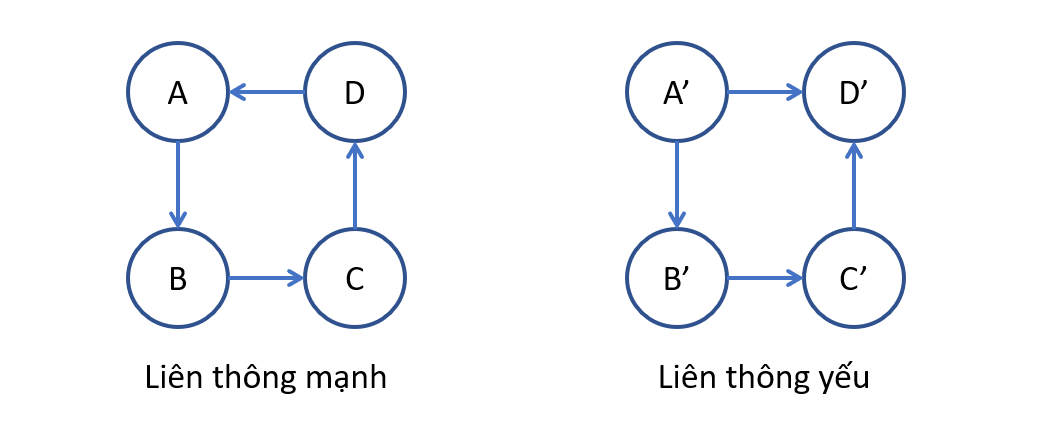
Liên thông mạnh: Đồ thị có hướng $G = (V, A)$ được gọi là liên thông mạnh nếu luôn tìm được đường đi giữa hai đỉnh bất kỳ của nó.
Liên thông yếu: Đồ thị có hướng $G = (V, A)$ được gọi là liên thông yếu nếu đồ thị vô hướng tương ứng với nó là vô hướng liên thông.

(!)Note: Đồ thị liên thông mạnh thì cũng liên thông yếu.

📝 Tham khảo thuật toán đếm số TPLT mạnh của đồ thị có hướng (Tarjan):

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
int m,n; 
vector<int> a[N];  
stack<int> st; 
int id[N], min_id[N]; 
bool visited[N]; 
//Nhập thông tin và biểu diễn đồ thị dạng danh sách kề
void inp()
{
    cin >> n >> m; 
    for (int i = 0; i < m; ++i) {
        int x,y; 
        cin >> x >> y; 
        a[x].push_back(y); 
    } 
    fill(id , id + N , 0); 
    fill(visited , visited + N , 0); 
} 
int cnt = 0, cc = 0; 
void dfs(int u)   //Hàm dfs phối hợp thêm logic của Thuật toán tarjan 
{
    id[u] = min_id[u] = ++cnt; 
    st.push(u); 
    for (auto x : a[u]) 
    {
        if (visited[x]) continue; 
        if (id[x]) min_id[u] = min(min_id[u] , id[x]); 
        else {
            dfs(x); 
            min_id[u] = min(min_id[u] , min_id[x]);  
        }
    } 
    if (id[u] == min_id[u]) 
    {
        ++cc; 
        int line = -1; 
        while (line != u) 
        {
            line = st.top(); 
            visited[line] = 1; 
            st.pop(); 
        }
    }
}
void solve()
{
    inp();    //Nhập thông tin cho đồ hị 
    for (int i = 1; i <= n; ++i) if (!id[i]) dfs(i); 
    cout << cc << endl;  
}
int main()
{
    solve();

}

8.1.6. Đẳng cấu đồ thị

Hai đồ thị G1 và G2 được gọi là đẳng cấu với nhau, ký hiệu là G1 ≈ G2, nếu có thể vẽ lại (bằng cách dời đỉnh, dời cạnh...) sao cho hai đồ thị này có hình vẽ y hệt nhau.

Đặc điểm

Cùng số đỉnh.
Cùng số đỉnh bậc $k$ , mọi $k$ nguyên dương ≥ 0.
Cùng số cạnh.
Cùng số thành phần.

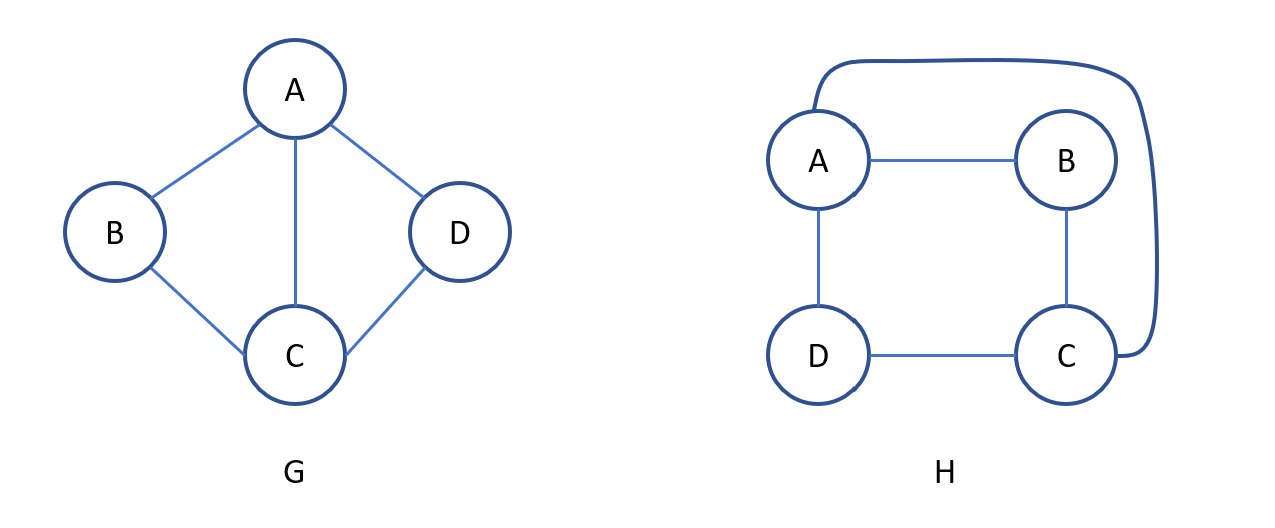
Nhận xét: Hai đồ thị G và H được gọi là đẳng cấu

8.1.7. Ứng dụng

Mô hình đồ thị xuất hiện rất nhiều xung quanh ta, trong nhiều lĩnh vực của cuộc sống hằng ngày, các bạn có thể tham khảo một số ứng dụng phổ biến của nó được trình bày ở bằng bên dưới:

Lĩnh vực	Ứng dụng cụ thể
Giao thông	- Tìm đường đi ngắn nhất giữa hai địa điểm (GPS, Google Maps)
Mạng xã hội	- Phân tích mối quan hệ giữa người dùng (Facebook, Twitter)
Tin học	- Cấu trúc dữ liệu (bộ nhớ, cây thư mục, mạng máy tính)
Điện lực, viễn thông	- Thiết kế mạng lưới truyền tải điện, mạng điện thoại
Lập lịch	- Phân công công việc, lịch học, thi cử (sử dụng đồ thị hai phía, đồ thị lưỡng phân)
Sinh học, y học	- Mô hình hóa mạng gen, mạng nơ-ron thần kinh
Công nghiệp & logistics	- Tối ưu hóa tuyến giao hàng, chuỗi cung ứng
AI & Machine Learning	- Mạng nơ-ron nhân tạo, đồ thị tri thức
Tài chính	- Phân tích thị trường, mối liên hệ giữa các cổ phiếu
Truyền thông & báo chí	- Truy vết thông tin giả qua các mạng liên kết

Bài viết tham khảo:

8.2. Giới thiệu các thuật toán trên đồ thị

8.2.1. Tổ chức dữ liệu

8.2.1.1. Ma trận kề

Ma trận kề là một cách biểu diễn đồ thị trên máy tính bằng ma trận vuông cấp $n$ , trong đó $n$ là số lượng đỉnh trong đồ thị (các đỉnh được đánh số từ 1 đến $n$ ). Các phần tử của ma trận có giá trị 0 hoặc 1 thể hiện mối liên kết giữa các đỉnh.

Nhận xét chung:

A[i][j] = 1: tồn tại đường đi giữa hai đỉnh i và j
A[i][j] = 0: không tồn tại đường đi giữa hai đỉnh i và j
Nếu cạnh nối (i, j) có trọng số là w thì đặt A[i][j] = w

Xét ma trận kề của đồ thị vô hướng:

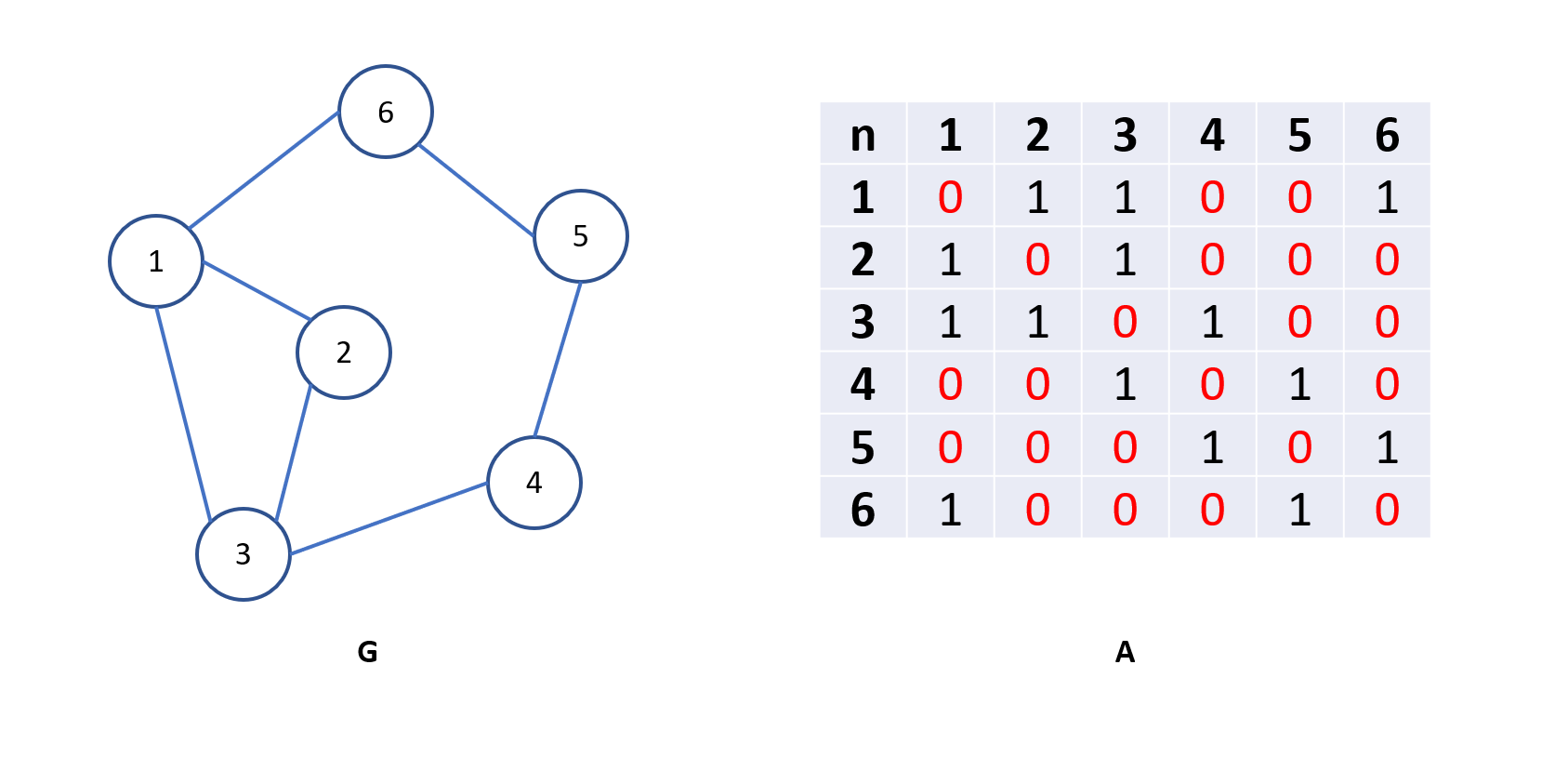
Tính chất:

Ma trận kề của đồ thị vô hướng là một ma trận đối xứng
Tổng các phần tử trên ma trận bằng 2 lần số cạnh
Tổng các phần tử trên hàng thứ k hoặc cột thứ k là bậc của đỉnh k

Xét ma trận kề của đồ thị có hướng:

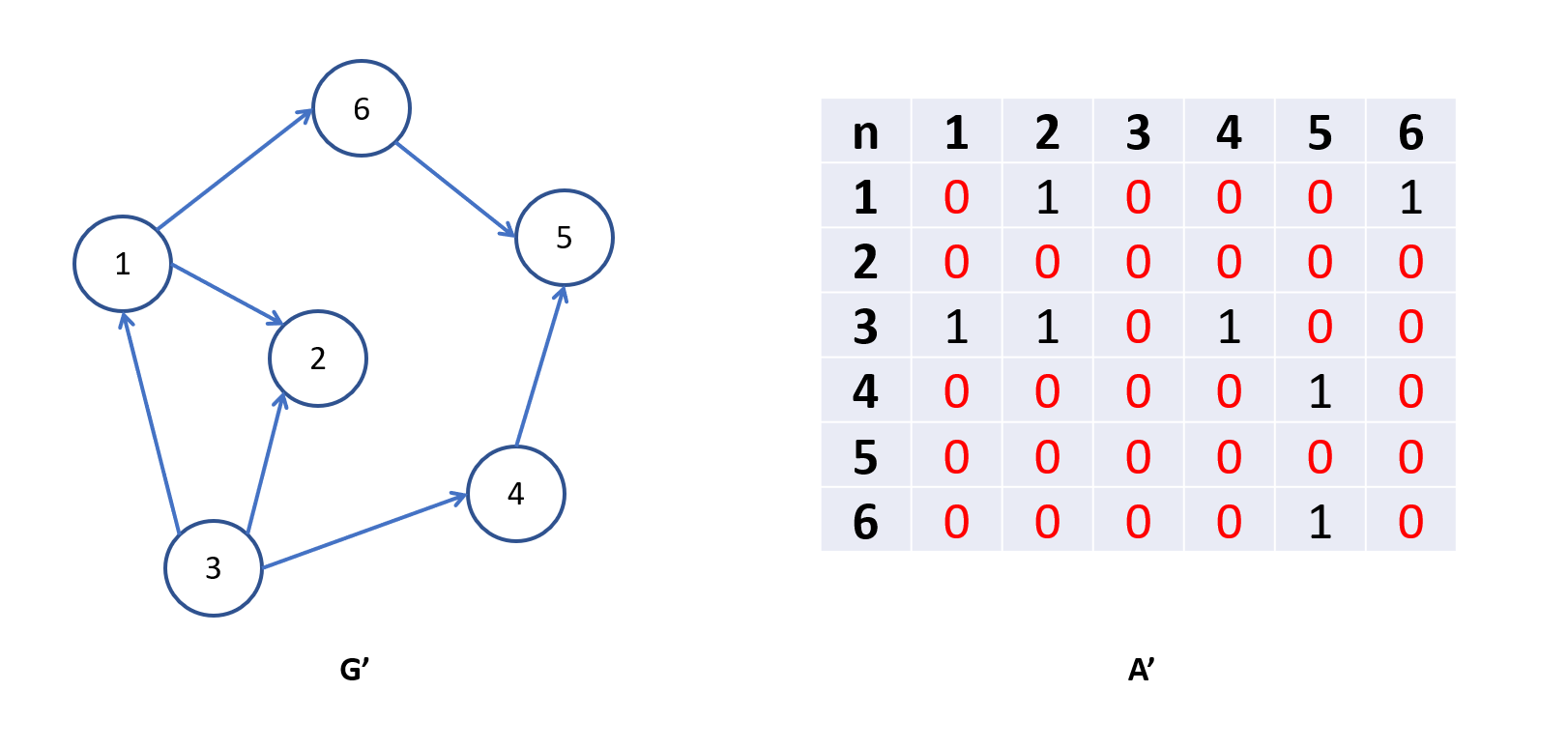
Tính chất:

Ma trận kề có thể không đối xứng
Tổng các phần tử trên ma trận bằng số cạnh
Tổng các phần tử trên hàng thứ $k$ là tổng số bậc ra của đỉnh $k$
Tổng các phần tử trên cột thứ $k$ là tổng số bậc vào của đỉnh $k$

Ưu điểm

Dễ dàng thể hiện quan hệ kề, có thể nhìn thấy ngay dựa vào giá trị của các phần tử

Nhược điểm Việc lưu trữ và tính toán sẽ tiêu hao rất nhiều tài nguyên bộ nhớ, đặc biệt với các đồ thị lớn

Không thích hợp khi xử lí đồ thị thưa

8.2.1.2. Danh sách cạnh

Danh sách cạnh gồm một danh sách các cặp đỉnh, mỗi cặp đỉnh tương ứng với một cạnh trong đồ thị. Mỗi cạnh được biểu diễn bằng hai đỉnh mà nó kết nối. Nếu giả thuyết đầu vào là đồ thị có n đỉnh, m cạnh ta thường biểu diễn đồ thị dưới dạng danh sách cạnh (thông qua mảng hay danh sách liên kết).

Đồ thị vô hướng: Nếu tồn tại cạnh giữa hai điểm $i$ và $j$ ta chỉ cần liệt kê cạnh (i, j) (khi $i$ < $j$ ) hoặc ( $j$ , $i$ ) (khi $j$ < $i$ ) theo thứ tự tăng dần của đỉnh đầu các cạnh.

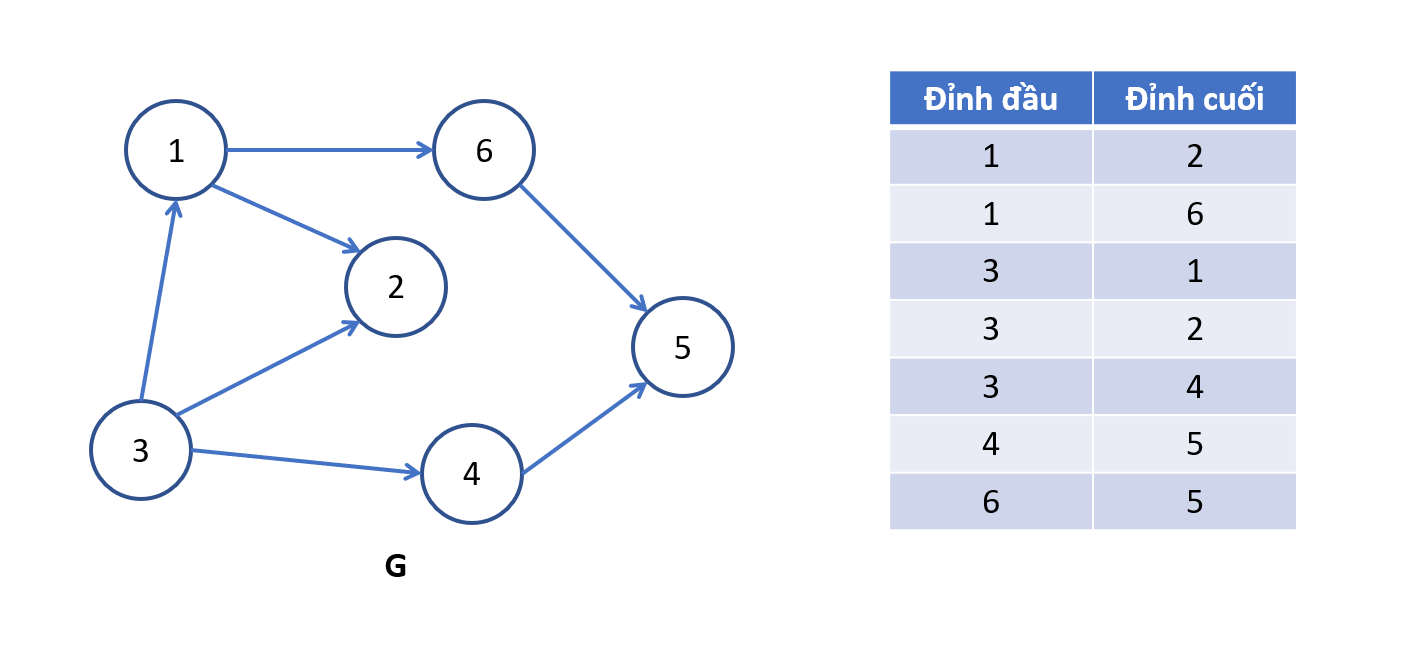
Ngược lại, với đồ thị có hướng, nếu có đường đi từ đỉnh $i$ đến đỉnh $j$ Đồ thị có trọng số: Khi có trọng số, biểu diễn trên máy tính ta có thể tạo struct lưu 3 thành phần của danh sách là: Dinh_dau, Dinh_cuoi, Trong_so.

Ưu điểm

Tiết kiệm không gian lưu trữ, chỉ cần lưu các cạnh thực sự xuất hiện trong đồ thị.
Thích hợp cho các thuật toán xử lí đồ thị, tăng hiệu quả xử lí thuật toán

Nhược điểm

So với ma trận kề, việc truy cập, tìm kiếm hai cạnh có thể tốn thời gian hơn, lên đến O(N) cho việc duyệt danh sách cạnh.

8.2.1.3. Danh sách kề

là danh sách các mảng hoặc danh sách liên kết, trong đó mỗi phần tử tương ứng với một đỉnh trong đồ thị. Mỗi phần tử trong danh sách này chứa thông tin về các đỉnh kề của đỉnh tương ứng đó. Trong C++ ta sử dụng một mảng vector để biểu diễn danh sách kề.

Đồ thi vô hướng

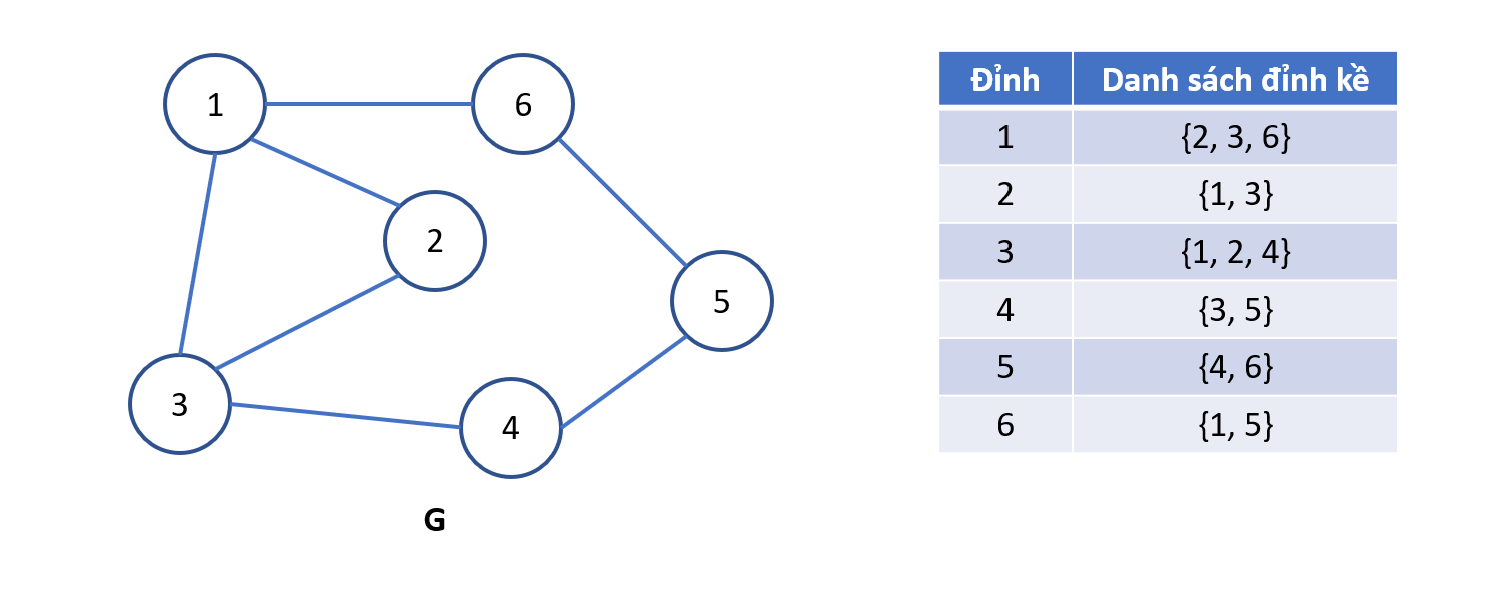
Đồ thị có hướng

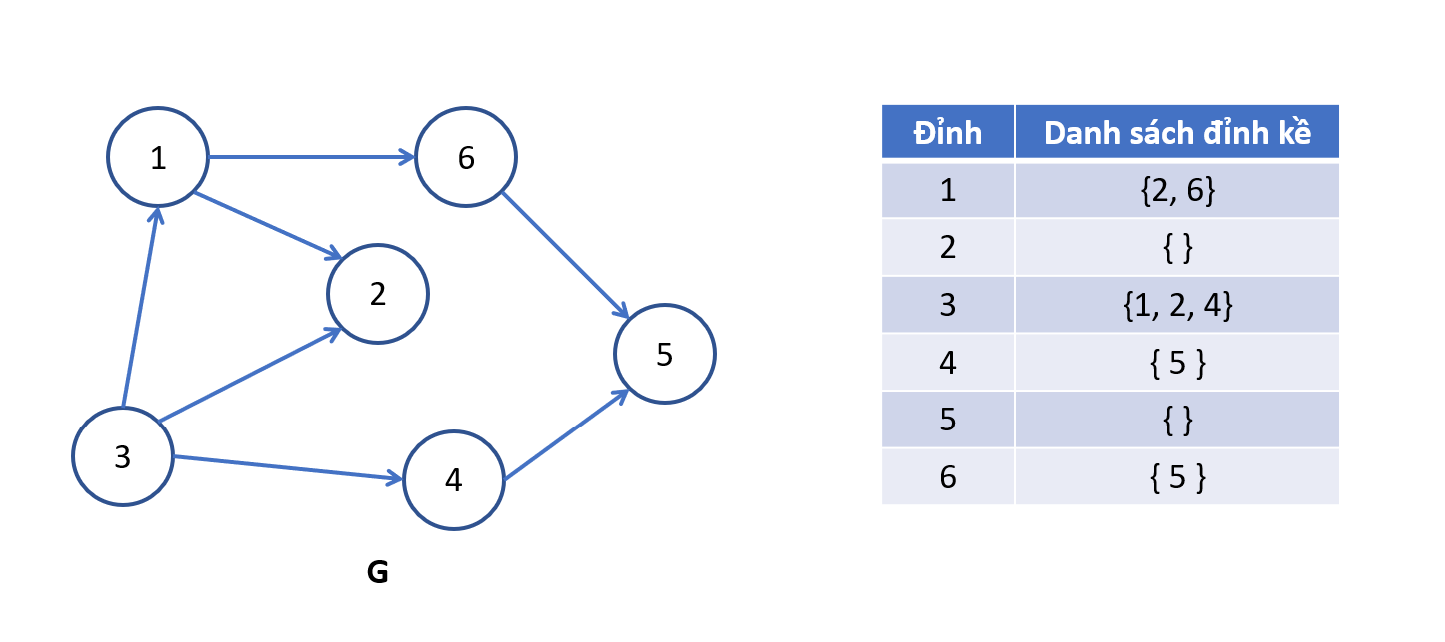
Ưu điểm

Tối ưu về phương pháp biểu diễn, được sử dụng rộng rãi trong các giải thuật về đồ thị
Truy cập nhanh đến đỉnh kề: dễ dàng truy cập đến các đỉnh kề của một đỉnh cụ thể

Nhược điểm

Không thích hợp cho đồ thị khác đồ thị thưa: danh sách kề có thể tốn nhiều không gian lưu trữ hơn so với ma trận kề.

Nhập thông tin cho đồ thị: Thông thường, bài toán sẽ cho chúng ta nhập vào danh sách cạnh của đồ thị, chúng ta sẽ chuyển đổi và lưu trữ đồ thị dưới dạng danh sách kề tương ứng.

#include <iostream>
#include <vector> 
using namespace std; 
const int N = 1e6; 
vector<int> adj[N];  //Danh sách kề
int m, n; //m là số lượng cạnh trong danh sách cạnh, n là số đỉnh của đồ thị 
int main() 
{
  cout << "Nhap so canh va so dinh: "; cin >> n >> m; 
  for (int i = 0; i < m; ++i) 
  {
    int x,y; 
    cin >> x >> y;  //Nhập danh sách cạnh 
    adj[x].push_back(y); 
    adj[y].push_back(x); 
    //Chuyển đổi thành danh sách kề của đồ thị
    //Nếu là đồ thị vô hướng, vì tồn tại đường đi hai chiều giữa 2 đỉnh x và y nên ta thực hiện adj[x].push_back(y); adj[y].push_back(x);  
    //Nếu là đồ thị có hướng, chỉ tồn tại đường đi từ đỉnh x đến y, ta chỉ thực hiện adj[x].push_back(y); 
  } 
}

Note: Có thể kết hợp thêm các kiểu dữ liệu STL như pair, set, map,... để mở rộng và tối ưu hóa lưu trữ

8.2.2. Duyệt DFS

Tìm kiếm theo chiều sâu (DFS) là một thuật toán để duyệt qua hoặc tìm kiếm cấu trúc dữ liệu dạng cây hoặc đồ thị. Thuật toán bắt đầu tại nút gốc (chọn một số nút tùy ý làm nút gốc trong trường hợp đồ thị) và kiểm tra từng nhánh càng xa càng tốt trước khi quay lui.

🦉 Thuật toán

👉 B1. Sử dụng đệ quy (quả bóng dây).

👉 B2. Đánh dấu mỗi đỉnh đã được truy cập (và giữ thông tin về cạnh đã đi để truy cập đỉnh đó).

👉 B3. Trả về (đi ngược lại các bước đã đi) khi không có tùy chọn chưa được truy cập.

Bạn có thể xem mô phỏng thuật toán DFS tại đây

🦉 Cấu trúc dữ liệu

bool vísited[] để đánh dấu các đỉnh đã được truy cập.
vector<int> adj[] lưu giữ thông tin đồ thị dưới dạng danh sách kề

Bài toán Cho một đồ thị vô hướng G. In ra thứ tự đỉnh được duyệt bằng thụât toán DFS

#include <bits/stdc++.h> 
using namespace std; 
int m,n; 
const int N = 1e5; 
vector<int> adj[N]; //Biểu diễn danh sách kề  
bool visited[N]; 
void inp() 
{
    cin >> n >> m; 
    for (int i = 0; i < m; ++i) {
        int x,y; 
        cin >> x >> y;  //Nhập vào danh sách cạnh của đồ thị
        adj[x].push_back(y);   //Biểu diễn thành danh sách kề của đồ thị 
        adj[y].push_back(x); 
    } 
    fill(visited , visited + N , 0); 
}
void dfs(int u) 
{
    visited[u] = 1;   //Đánh dấu đỉnh đã thăm rồi 
    cout << u << ' ';    //In ra đỉnh đang thăm  
    for (auto x : adj[u]) if (!visited[x]) dfs(x); //Duyệt qua DS kề của đỉnh đang được thăm hiện tại, nếu phát hiện đỉnh chưa được thăm thì gọi dfs để thăm đỉnh đó   
}
int main() 
{
    inp(); //Nhập dữ liệu cho đồ thị 
    for (int i = 1; i <= n; ++i) if (!visited[i]) dfs(i); 
}

Chúng ta có thể thực hiện khử đệ quy thuật toán DFS bằng stack, phân biệt với thuật toán BFS, bản chất cũng là đệ quy nhưng được khử bằng queue.

🦉 Độ phức tạp

Độ phức tạp thời gian của thuật toán DFS được biểu diễn dưới dạng $O(V + E)$ , trong đó $V$ là số nút và $E$ là số cạnh. Độ phức tạp không gian của thuật toán là $O(V)$ .

🦉 Ứng dụng

Thuật tán DFS đuợc ứng dụng để giải quyết rất nhiều bài toán khác nhau trong đồ thị, chúng ta có thể liệt kê một số ứng dụng sau đây:

Sắp xếp topo, phát hiện chu trình, thành phần liên thông của đồ thị cũng như nâng cấp, giải quyết các bài toán chỉ có một phương pháp giải (backtracking): xếp hậu, sudoku, tô màu đồ thị, sinh hoán vị, tổ hợp...

Phân tích luồng điều khiển trong chương trình (control flow analysis), xem có đường nào có thể dẫn tới lỗ hổng bảo mật không, khám phá các trang web liên kết theo chiều sâu trước, thay vì quét toàn bộ từng tầng (như BFS).
Duyệt thư mục lồng nhau cũng thường sử dụng DFS đi sâu vào từng thư mục con trước

📝 Tham khảo: Thuật toán DFS trên lưới ô vuông

Đề bài – Kiểm tra khả năng tồn tại đường đi trong lưới bằng DFS

Cho một ma trận nhị phân A kích thước N x N, trong đó mỗi phần tử A[i][j] nhận một trong hai giá trị:

1: ô (i, j) có thể đi vào (ô trống),
0: ô (i, j) không thể đi vào (chướng ngại vật).

Bạn được cung cấp hai điểm:

Điểm bắt đầu: start = (x1, y1)
Điểm kết thúc: end = (x2, y2)

Yêu cầu:

Hãy kiểm tra xem có tồn tại một đường đi hợp lệ từ điểm bắt đầu đến điểm kết thúc hay không.

Quy tắc di chuyển:

Mỗi bước, bạn có thể di chuyển lên, xuống, trái, hoặc phải (không được đi chéo).
Chỉ được đi qua các ô có giá trị 1.

Ràng buộc:

0 ≤ x1, x2, y1, y2 < N
1 ≤ N ≤ 1000
Ma trận A được biểu diễn dưới dạng mảng hai chiều.

Đầu ra:

In "YES" nếu tồn tại đường đi từ start đến end.
In "NO" nếu không tồn tại đường đi nào thỏa mãn điều kiện.

#include <bits/stdc++.h>
using namespace std;
int X[] = {0 , 0 , -1 , 1};   //Mảng thể hiện bước di chuyển 
int Y[] = {1 , -1, 0, 0};     //Trên, dưới, trái, phải 
int x_1, y_1, x_2, y_2;
const int N = 1000;
int a[N][N];
int n; //Kích thước lưới
void inp()
{
    cin >> n;  //Kích thước lưới 
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < n; ++j) cin >> a[i][j];   //Nhập giá trị từng ô trong lưới 
}
bool isValid(int x, int y) 
{
    if (x >= 0 && x < n && y >= 0 && y < n) return 1; 
    return 0; 
}
bool dfs_net(int x, int y)
{
    if (x == x_2 && y == y_2) return 1;
    a[x][y] = -1; //Đánh dấu ô đã đi qua 
    for (int k = 0; k < 4; ++k)
    {
      //Tính toán vị trí ô tiếp theo sẽ đi qua 
        int next_x = x + X[k];  
        int next_y = y + Y[k];
        if (next_x >= 0 && next_x < n && next_y >= 0 && next_y < n && a[next_x][next_y] != -1) return dfs_net(x , y); //Gọi dfs để đi qua ô hợp lệ 
    }
    return 0;
}
void solve()
{
    inp();
    cout << "Nhap vi tri bat dau: "; cin >> x_1 >> y_1;  //Vị trí bắt đầu 
    cout << "Nhap vi tri ket thuc: "; cin >> x_2 >> y_2;   //Vị trí kết thúc 
    if (isValid(x_1 , y_1) && isValid(x_2 , y_2)) {   //Vị trí nhập vào không hợp lệ 
         cout << "Vi tri khoi tao khong hop le"; 
         return; 
    } 
    bool ans = dfs_net(x_1 , y_1); 
    if (ans) cout << "YES"; 
    else cout << "NO"; 
}
int main()
{
    solve();
}

8.2.3. Duyệt BFS

Tìm kiếm theo chiều rộng (BFS) là một thuật toán để duyệt đồ trong đó, các đỉnh gần đỉnh xuất phát hơn sẽ được duyệt trước. Khác với DFS sử dụng satck hoặc đệ quy, thuật toán BFS sử dụng cấu trúc dữ liệu hàng đợi (queue) để cài đặt

🦉 Thuật toán

👉 B1. Lấy đỉnh v ở đầu hàng đợi và đánh dấu cho biết đỉnh v đã được thăm
👉 B2. Tiếp theo, ta tiến hành thăm danh sách kề / các đỉnh kề của đỉnh v. Thêm tắt cả các đỉnh này vào sau cùng của hàng đợi và đánh dấu chúng đã thăm

Quá trình lặp đi lặp lại đến khi hàng đợi rỗng

Các bạn có thể xem mô phòng thuật toán bfs tại đây

🦉 Cấu trúc dữ liệu

bool vísited[] để đánh dấu các đỉnh đã được truy cập.
vector<int> adj[] lưu giữ thông tin đồ thị dưới dạng danh sách kề

Bài toán Cho một đồ thị vô hướng G. In ra thứ tự đỉnh được duyệt bằng thuật toán BFS

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5;
vector<int> a[N];
bool visited[N];
int m,n;

void inp()
{
    cin >> n >> m; //Sổ đỉnh và số phần tử của danh sách cạnh nhập vào
    for (int i = 0; i < m; ++i) {
        int x,y;
        cin >> x >> y; //Nhập vào danh sách cạnh của đồ thị
        a[x].push_back(y); //Biểu diễn danh sách cạnh thành danh sách kề 
        a[y].push_back(x);
    }
    fill(visited , visited + N , 0);
}
void bfs(int u)
{
    queue<int> q;
    q.push(u); //Thêm phần tử vào hàng đợi 
    visited[u] = 1;
    cout << u << ' ';
    while (q.size())  //Lặp đến khi hàng đợi rỗng 
    {
        int v = q.front(); q.pop();  //Lấy đỉnh ở đầu hàng đợi ra khỏi hàng đợi 
        cout << v << ' ';  //In đỉnh đang được thăm (ở đầu hàng đợi)
        for (auto x : a[v]) if (!visited[x]) {  //Duyệt qua danh sách kề của đỉnh và đưa vào sau hàng đợi các đỉnh chưa được hăm 
            visited[x] = 1;
            q.push(x);
        }
    }
}
int main()
{
    inp();
    for (int i = 1; i <= n; ++i) if (!visited[i]) bfs(i);
}

🦉 Độ phức tạp

Nhìn chung, nếu biểu diễn bằng danh sách kề, độ phức tạp của thuật toán sẽ là O(V + E), đây là các cài đặt tốt nhất. Tuy nhiên, nếu biểu diễn bằng ma trận kề thì ta phải thực hiện duyệt qua V đinh, tốn thời gian $O(V)$ cho mỗi đỉnh. Ở mỗi đỉnh ta lại phải duyệt toàn bộ các đỉnh còn lại để xác định được đỉnh con của V, độ phức tạp có thể lên tới $O(V^2)$

🦉 Ứng dụng

Tìm kiếm theo chiều rộng là thuật toán chính được sử dụng để lập chỉ mục các trang web. Thuật toán BFS bắt đầu từ trang nguồn và đi theo tất cả các liên kết được liên kết với nó.
Các hệ thống mạng xã hội như Facebook, Linkedln thường gợi ý danh sách những người bạn mới dựa trên kết quả duyệt BFS theo từng cấp độ trong danh sách bạn bè của chính chủ.
Ngoài ra, BFS còn được sử dụng rộng rãi trong các bài toán lien quan đến đồ thị như: xây dựng sắp xếp topo, mê cung 2D, sudoku. Kinh điển là bài toán tìm đường đi ngắn nhất trên đồ thị không trọng số

📝 Tham khảo: Ứng dụng BFS trong tìm đường đi ngắn nhất trên đồ thị không trọng số

Một số bài yêu cầu tìm số bước ít nhất (hoặc đường đi ngắn nhất) từ điểm đầu đến điểm cuối. Bên cạnh đó, đường đi giữa điểm bất kì thường có chung trọng số (và thường là ). Phổ biến nhất là dạng bài cho bảng A, có những ô đi qua được và những ô không đi qua được. Bảng này có thể là mê cung, sơ đồ, các thành phố hoặc các thứ các thứ tương đương và yêu cầu ta tìm kiếm đường đi ngắn nhất. Có thể nói đây là những bài toán kinh điển.

Cho đồ thị vô hướng G = (V , E). Tìm đường đi ngắn nhất từ đỉnh 1 đến tất cả các đỉnh trong đồ thị

#include <iostream>
#include <queue>
#include <vector>
#include <math.h>
using namespace std;
const int N = 1e6;
const int INF = 1e8;
vector<int> a[N];
int m,n;
bool visited[N];
int dist[N];  //dist[i]: Độ dài đường đi ngắn nhất từ đỉnh 1 đến đỉnh i 
void inp()
{
    cout << "Nhap so dinh va so canh: ";
    cin >> n >> m;
    for (int i = 0; i < m; ++i) {
        int x,y;
        cin >> x >> y; //Nhập danh sách cạnh 
        a[x].push_back(y);  //Chuyển đổi đồ thị sang danh sách kề 
        a[y].push_back(x);
    }
    fill(visited , visited + N , 1);
}
void bfs(int u)
{
    queue<int> q;  //Hàng đợi cài đặt thuật toán BFS 
    q.push(u);
    visited[u] = 1;
    while (q.size())
    {
        int v = q.front(); q.pop();
        visited[v] = 1;
        for (auto x : a[v]) if (!visited[x]) {
            dist[x] = min(dist[x] , 1 + dist[v]);  
            /*Vì chúng ta di chuyển từ đỉnh v đến đỉnh x nên ta cập nhật Khoảng cách ngắn nhất từ đỉnh 1 đến đỉnh x sẽ bằng Khoảng cách 
            ngắn nhất từ đỉnh 1 đến v cộng thêm cho 1 */
            visited[x] = 1;  //Đánh dấu đỉnh x đã thăm 
            q.push(x);
        }
    }
}
void solve()
{
    inp();
    fill(dist , dist + N , INF); //Khởi tạo giá trị ban đầu cho mảng khoảng cách. 
    //Vì tìm độ dài đường đi nhỏ nhất nên ta khởi tạo mặc định dist[i] = INF (một số rất lớn) để thuận tiện cho việc tìm min. 
    dist[1] = 0;  //Khoảng cách ngắn nhất từ đỉnh 1 đến đỉnh 1 là 0. 
    bfs(1); //Bắt đầu duyệt BFS từ đỉnh 1. 
}

int main()
{
    solve();
    cout << "\nKhoang cach nho nhat tu dinh 1 den cac dinh tuong ung la: " << endl;
    for (int i = 1; i <= n; ++i)
        if (dist[i] == INF) cout << "INF" << ' ';
        else cout << dist[i] << ' ';
}

8.2.4. Thuật toán tìm đường đi ngắn nhất Djikstra

8.2.4.1. Bài toán dẫn nhập

Thuật toán Dijkstra, mang tên của nhà khoa học máy tính người Hà Lan Edsger Dijkstra vào năm 1956, khi làm việc tại trung tâm Toán học Amsterdam năm 1956 với tư cách là một lập trình viên, thuật toán được sáng tạo trong 20 phút vào một buổi sáng đi mua sắm ở Amsterdam và được ấn bản 3 năm sau đó, đây là một thuật toán giải quyết bài toán đường đi ngắn nhất từ một đỉnh đến các đỉnh còn lại của đồ thị có hướng không có cạnh mang trọng số không âm.

Các bạn có thể xem mô phỏng thuật toán tại đây

🦉 Ý tưởng thuật toán

Thuật toán Djikstra được xây dựng dựa trên tư tưởng tham lam (greedy), luôn chọn đỉnh có khoảng cách nhỏ nhất chưa được xét tới.

Bắt đầu từ đỉnh nguồn, gán khoảng cách của nó là 0, các đỉnh còn lại là vô cùng.
Duyệt các đỉnh theo thứ tự khoảng cách ngắn nhất hiện tại.
Với mỗi đỉnh được chọn, duyệt các đỉnh kề chưa được xét:
- Nếu đường đi qua đỉnh hiện tại ngắn hơn, cập nhật khoảng cách.
Lặp lại quá trình cho đến khi tất cả các đỉnh được xét.

🦉 Cấu trúc dữ liệu

distance[]: mảng lưu khoảng cách ngắn nhất từ nguồn đến các đỉnh.
visited[]: mảng đánh dấu đỉnh đã được xử lý.
hàng đợi ưu tiên (priority queue) hoặc tập hợp có sắp xếp (set) để chọn nhanh đỉnh có khoảng cách nhỏ nhất.

#include <bits/stdc++.h> 
using namespace std; 
int m, n; 
const int N = 1e5;          // Số lượng đỉnh tối đa
const int INF = 1e8;        // Giá trị vô cực đại để khởi tạo khoảng cách
vector<pair<int, int>> a[N]; // Danh sách kề: a[x] lưu các cặp (đỉnh kế, trọng số cạnh)
int dist[N];                 // Mảng lưu khoảng cách ngắn nhất từ đỉnh bắt đầu đến các đỉnh

// Hàm nhập dữ liệu đồ thị
void inp() 
{
    cin >> n >> m;          // Nhập số đỉnh và số cạnh
    for (int i = 0; i < m; ++i) {
        int x, y, w; 
        cin >> x >> y >> w; 
        // Thêm cạnh x -> y với trọng số w
        a[x].push_back(make_pair(y, w)); 
        // Thêm cạnh y -> x với trọng số w (vì đây là đồ thị vô hướng)
        a[y].push_back(make_pair(x, w)); 
    } 
    // Khởi tạo khoảng cách tất cả các đỉnh bằng vô cực
    fill(dist, dist + N, INF); 
}
// Thuật toán Dijkstra tìm đường đi ngắn nhất từ đỉnh u
void djikstra(int u) 
{
    dist[u] = 0; // Khoảng cách từ u đến u bằng 0
    // Hàng đợi ưu tiên lưu cặp (khoảng cách, đỉnh), ưu tiên khoảng cách nhỏ nhất
    priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> q; 
    q.push({0, u}); // Đưa đỉnh bắt đầu vào hàng đợi 
    while (q.size())  // Lặp đến khi không còn đỉnh nào để xử lý
    {
        pair<int, int> marked = q.top(); q.pop(); 
        int v = marked.second;   // Đỉnh hiện tại đang xét
        int len = marked.first;  // Khoảng cách đến đỉnh v hiện tại

        if (dist[v] < len) continue; // Nếu khoảng cách này không phải nhỏ nhất thì bỏ qua

        // Duyệt tất cả các đỉnh kề của v
        for (auto it : a[v])  
        {
            int x = it.first;  // Đỉnh kế tiếp
            int w = it.second; // Trọng số cạnh v -> x

            // Nếu tìm được đường đi ngắn hơn đến x qua v
            if (dist[x] > dist[v] + w) {
                dist[x] = dist[v] + w;     // Cập nhật khoảng cách
                q.push({dist[x], x});      // Đưa đỉnh x vào hàng đợi để xử lý tiếp
            } 
        }
    }
}

// Hàm giải quyết bài toán
void solve() 
{
    inp(); // Nhập dữ liệu đồ thị
    int u; 
    cout << "Nhap dinh bat dau: "; 
    cin >> u; // Nhập đỉnh bắt đầu
    djikstra(u); // Tính khoảng cách ngắn nhất từ đỉnh u
    // In kết quả khoảng cách từ u đến tất cả các đỉnh
    for (int i = 1; i <= n; ++i) {
        cout << "Khoang cach nho nhat tu dinh " << u << " den dinh " << i << " la: " << dist[i] << endl;
    }
} 
int main() 
{
    solve(); // Gọi hàm giải
}

8.3. Ứng dụng đồ thị

8.3.1. Bài toán Tô màu bản đồ

🦉 Đề bài

(Trích đề thi thử Cấu trúc dữ liệu và giải thuật - UIT - HK2 năm học 2021-2022, và phát triển thêm)

Cho bài toán "Tô màu bản đồ" được đặt ra như sau: Có một bản đồ các quốc gia trên thế giới, ta muốn tô màu các quốc gia này sao cho hai nước có cùng ranh giới được tô khác màu nhau. Yêu cầu tìm cách tô sao cho số màu sử dụng là ít nhất.

Bài toán có thể được mô hình hóa thành một bài toán trên đồ thị, khi đó:

Mỗi nước trên bản đồ là một đỉnh của đồ thị
Hai nước láng giềng tương ứng với hai đỉnh kề nhau được nối với nhau bằng một cạnh
Bài toán trở thành: tô màu các đỉnh của đồ thị sao cho mỗi đỉnh chỉ được tô một màu, hai đỉnh kề nhau có màu khác nhau và số màu sử dụng là ít nhất.

Giả sử input đầu vào:

15
Viet_Nam Lao
Viet_Nam Trung_Quoc
Thai_Lan Lao
...
Campuchia Thai_Lan

Dòng đầu: số cạnh e của đồ thị
Trong e dòng tiếp theo: mỗi dòng chứa 2 chuỗi u và i, thể hiện có cạnh nối từ đỉnh u sang đỉnh i

Lưu ý: Không biết trước số đỉnh và danh sách các đỉnh

🦉 Yêu cầu

a. Xây dựng cấu trúc dữ liệu thích hợp để biểu diễn đồ thị
b. Viết hàm nhập đồ thị
c. Xuất tên tất cả các nước và các nước láng giềng của nó

🦉 Lời giải

a. Cấu trúc dữ liệu

map<string, set<string>> listCountry;

Giải thích:

Sử dụng map với:
- key (string): tên quốc gia
- value (set<string>): danh sách các nước láng giềng
Ưu điểm:
- Truy xuất hiệu quả bằng tên quốc gia
- set tự động loại bỏ trùng lặp và sắp xếp
- Dễ dàng thêm/xóa/quản lý các cạnh

b. Hàm nhập đồ thị

void inputGraph() {
    int e;
    cin >> e;
    for (int j = 0; j < e; j++) {
        string u, i;
        cin >> u >> i;
        listCountry[u].insert(i);
        listCountry[i].insert(u);
    }
}

c. Xuất danh sách quốc gia và láng giềng

void printCountriesAndNeighbors() {
    for (auto x : listCountry) {
        cout << x.first << "'s neighbors: ";
        for (auto y : x.second) {
            cout << y << " ";
        }
        cout << endl;
    }
}

Chương trình hoàn chỉnh

#include <iostream>
#include <map>
#include <set>
#include <string>
using namespace std;

map<string, set<string>> listCountry;

void inputGraph() {
    int e;
    cin >> e;
    for (int j = 0; j < e; j++) {
        string u, i;
        cin >> u >> i;
        listCountry[u].insert(i);
        listCountry[i].insert(u);
    }
}

void printCountriesAndNeighbors() {
    for (auto x : listCountry) {
        cout << x.first << "'s neighbors: ";
        for (auto y : x.second) {
            cout << y << " ";
        }
        cout << endl;
    }
}

int main() 
{
    inputGraph();
    printCountriesAndNeighbors();
    return 0;
}

🦉 Giải thích chi tiết

Cấu trúc dữ liệu:
- map cho phép truy xuất nhanh đến từng quốc gia bằng tên
- set đảm bảo:
  - Không lưu trùng láng giềng
  - Tự động sắp xếp (nếu cần)
  - Thao tác chèn/xóa hiệu quả
Hàm nhập:
- Với mỗi cạnh (u, i), thêm vào danh sách kề của cả 2 đỉnh
- Tự động tạo mới entry nếu quốc gia chưa tồn tại trong map
Hàm xuất:
- Dùng auto để duyệt qua map và set một cách ngắn gọn
- x.first: tên quốc gia
- x.second: set các láng giềng

Lưu ý: Chương trình này chưa xử lý bài toán tô màu, chỉ mới dừng ở bước xây dựng cấu trúc dữ liệu và nhập/xuất đồ thị.

8.1. Lý thuyết Đồ thị​

8.1.1. Khái niệm​

Đồ thị vô hướng (Undirected Graph)​

Đồ thị có hướng (Directed Graph)​

Đồ thị có trọng số (Weighted graph)​

8.1.2. Một số đồ thị đặc biệt​

8.1.3. Chu trình, đường đi​

8.1.4. Bậc của đỉnh (degree)​

8.1.5. Liên thông (connection)​

8.1.5.1. Đồ thị vô hướng​

8.1.5.2. Đồ thị có hướng​

8.1.6. Đẳng cấu đồ thị​

8.1.7. Ứng dụng​

Bài viết tham khảo:​

8.2. Giới thiệu các thuật toán trên đồ thị​

8.2.1. Tổ chức dữ liệu​

8.2.1.1. Ma trận kề​

8.2.1.2. Danh sách cạnh​

8.2.1.3. Danh sách kề​

8.2.2. Duyệt DFS​

🦉 Thuật toán​

🦉 Cấu trúc dữ liệu​

🦉 Độ phức tạp​

🦉 Ứng dụng​

Đề bài – Kiểm tra khả năng tồn tại đường đi trong lưới bằng DFS​

Yêu cầu:​

Ràng buộc:​

Đầu ra:​

8.2.3. Duyệt BFS​

🦉 Thuật toán​

🦉 Cấu trúc dữ liệu​

🦉 Độ phức tạp​

🦉 Ứng dụng​

8.2.4. Thuật toán tìm đường đi ngắn nhất Djikstra​

8.2.4.1. Bài toán dẫn nhập​

🦉 Ý tưởng thuật toán​

🦉 Cấu trúc dữ liệu​

8.3. Ứng dụng đồ thị​

8.3.1. Bài toán Tô màu bản đồ​

🦉 Đề bài​

🦉 Yêu cầu​

🦉 Lời giải​

a. Cấu trúc dữ liệu​

b. Hàm nhập đồ thị​

c. Xuất danh sách quốc gia và láng giềng​

Chương trình hoàn chỉnh​

🦉 Giải thích chi tiết​

8.1. Lý thuyết Đồ thị

8.1.1. Khái niệm

Đồ thị vô hướng (Undirected Graph)

Đồ thị có hướng (Directed Graph)

Đồ thị có trọng số (Weighted graph)

8.1.2. Một số đồ thị đặc biệt

8.1.3. Chu trình, đường đi

8.1.4. Bậc của đỉnh (degree)

8.1.5. Liên thông (connection)

8.1.5.1. Đồ thị vô hướng

8.1.5.2. Đồ thị có hướng

8.1.6. Đẳng cấu đồ thị

8.1.7. Ứng dụng

Bài viết tham khảo:

8.2. Giới thiệu các thuật toán trên đồ thị

8.2.1. Tổ chức dữ liệu

8.2.1.1. Ma trận kề

8.2.1.2. Danh sách cạnh

8.2.1.3. Danh sách kề

8.2.2. Duyệt DFS

🦉 Thuật toán

🦉 Cấu trúc dữ liệu

🦉 Độ phức tạp

🦉 Ứng dụng

Đề bài – Kiểm tra khả năng tồn tại đường đi trong lưới bằng DFS

Yêu cầu:

Ràng buộc:

Đầu ra:

8.2.3. Duyệt BFS

🦉 Thuật toán

🦉 Cấu trúc dữ liệu

🦉 Độ phức tạp

🦉 Ứng dụng

8.2.4. Thuật toán tìm đường đi ngắn nhất Djikstra

8.2.4.1. Bài toán dẫn nhập

🦉 Ý tưởng thuật toán

🦉 Cấu trúc dữ liệu

8.3. Ứng dụng đồ thị

8.3.1. Bài toán Tô màu bản đồ

🦉 Đề bài

🦉 Yêu cầu

🦉 Lời giải

a. Cấu trúc dữ liệu

b. Hàm nhập đồ thị

c. Xuất danh sách quốc gia và láng giềng

Chương trình hoàn chỉnh

🦉 Giải thích chi tiết